题目内容
已知△ABC的两条中线BD、CE相交于点G,若S△ABC=36,则S△DEG= .
考点:三角形的重心
专题:
分析:根据D,E分别是三角形的中点,得出G是三角形的重心,再利用重心的概念可得:2GD=AG进而得到S△ABG:S△ABE=2:3,再根据AE是△ABC的中线可得S△ABC=2S△ABE进而得到△ABG的面积.利用三角形的重心的定义得到DE是△ABC的中位线,利用三角形中位线的定理推知△DEG∽△BAG,由相似三角形的性质来求S△DEG.
解答: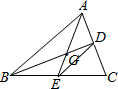 解:∵△ABC的两条中线AD、BE相交于点G,
解:∵△ABC的两条中线AD、BE相交于点G,
∴2GE=AG,
∴S△ABG=
S△ABE
∵AD是△ABC的中线,
∴S△ABC=2S△ABE.
∴S△ABG=
S△ABC=6.
依题意知,ED是△ABC的中位线,
则ED∥AB,
∴△DEG∽△ABG,
∴
=(
)2=(
)2=
,
则S△DEG=
S△ABG=
故答案为:
.
 解:∵△ABC的两条中线AD、BE相交于点G,
解:∵△ABC的两条中线AD、BE相交于点G,∴2GE=AG,
∴S△ABG=
| 2 |
| 3 |
∵AD是△ABC的中线,
∴S△ABC=2S△ABE.
∴S△ABG=
| 1 |
| 3 |
依题意知,ED是△ABC的中位线,
则ED∥AB,
∴△DEG∽△ABG,
∴
| S△DEG |
| S△ABG |
| EG |
| AG |
| 1 |
| 2 |
| 1 |
| 4 |
则S△DEG=
| 1 |
| 4 |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:此题考查了重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.

练习册系列答案
相关题目
某种药品原价为64元/盒,经过连续两次降价后售价为49元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
| A、64(1-x)2=64-49 |
| B、64(1-2x)=49 |
| C、64(1-x)2=49 |
| D、64(1-x2)=49 |
第6次全国人口普查显示,淮南市人口数约为2 330 000人,用科学记教法表示为( )
| A、2.33×106 |
| B、2.33×105 |
| C、23.3×105 |
| D、0.233×106 |
估算
的值(精确到0.1)约为( )
| 60 |
| A、3.7 | B、7.7 |
| C、7.6 | D、8.0 |
 如图,∠C=∠D=90°,求证:A,B,C,D四个点在以AB为直径的圆上.
如图,∠C=∠D=90°,求证:A,B,C,D四个点在以AB为直径的圆上.