题目内容
17．在Rt△ABC中，∠A=90°，AC=100m，∠C=50°，求AB．（保留1位小数）（sin50°≈0.7660，cos50°≈0.6428，tan50°≈1.1918）
分析 利用正切的定义求解即可．
解答 解：∵在Rt△ABC中，∠A=90°，AC=100m，∠C=50°，
∴AB=AC•tan∠C=100×tan50°=100×1.1918=119.18≈119.2．
点评 本题主要考查了解直角三角形，解题的关键是熟记正切的定义．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．
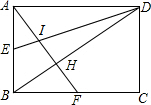如图，已知矩形ABCD，AB=6，BC=8，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（ ）
如图，已知矩形ABCD，AB=6，BC=8，E，F分别是AB，BC的中点，AF与DE相交于I，与BD相交于H，则四边形BEIH的面积为（ ）| A． | $\frac{38}{5}$ | B． | $\frac{28}{13}$ | C． | $\frac{28}{5}$ | D． | $\frac{48}{13}$ |
5．下列事件中，必然事件是（ ）
| A． | 抛掷一枚硬币，正面朝上 | |
| B． | 袋中只有4个球，且都是红球，任意摸出一球是红球 | |
| C． | 体育课上，小刚跑完1000米所用时间为1分钟 | |
| D． | 打开电视，正在播放广告 |
12．抛物线y=2（x+3）2+5的对称轴为（ ）
| A． | 直线x=3 | B． | 直线x=-3 | C． | 直线x=5 | D． | 直线x=-5 |
2．若点A（2，y1），B（-3，y2），C（-1，y3）三点在抛物线y=x2-4x+5的图象上，则y1、y2、y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y2＞y1＞y3 | C． | y2＞y3＞y1 | D． | y3＞y1＞y2 |
如图，在△ABC中，AE是中线，AD是角平分线，AF是高，∠B=30°，∠C=80°，BE=3，AF=2，填空：