题目内容
3.计算:(1)2$\sqrt{12}$+3$\sqrt{48}$;
(2)$\sqrt{32}$+3$\sqrt{\frac{1}{2}}$-2$\sqrt{\frac{1}{8}}$;
(3)$\frac{\sqrt{15×5}-\sqrt{48}-\sqrt{27}}{\sqrt{3}}$;
(4)$\frac{\sqrt{20}+\sqrt{80}}{\sqrt{5}}$.
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的化简,然后合并;
(3)先进行二次根式的化简,然后合并;
(4)先进行二次根式的化简,然后合并.
解答 解:(1)原式=4$\sqrt{3}$+12$\sqrt{3}$
=16$\sqrt{3}$;
(2)原式=4$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$-$\frac{\sqrt{2}}{2}$
=$\frac{7}{2}$$\sqrt{2}$+$\frac{3}{2}$$\sqrt{3}$;
(3)原式=$\frac{5\sqrt{3}-4\sqrt{3}-3\sqrt{3}}{\sqrt{3}}$
=-2;
(4)原式=$\sqrt{4}$+$\sqrt{16}$
=2+4
=6.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简与合并.

练习册系列答案
相关题目
14.若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2015-a-b的值是( )
| A. | 2017 | B. | 2018 | C. | 2019 | D. | 2020 |
11.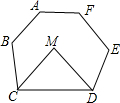 如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
 如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )
如图,在六边形ABCDEF中,CM,DM分别平分∠BCD和∠CDE,若∠A+∠B+∠E+∠F=510°,则∠M的度数为( )| A. | 85° | B. | 80° | C. | 75° | D. | 70° |
 的解集为
的解集为 ,则
,则 的取值范围是 __________
的取值范围是 __________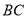 ∥
∥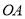 ,
, 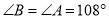 ,试解答下列问题:
,试解答下列问题: __________,则OB与AC的位置关系为__________
__________,则OB与AC的位置关系为__________
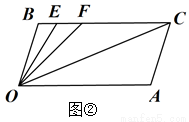
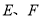 在线段
在线段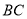 上,且满足
上,且满足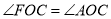 ,并且
,并且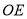 平分
平分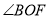 .则
.则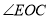 的度数等于_____________;
的度数等于_____________;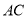 到如图③所示位置.
到如图③所示位置.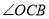 与
与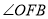 的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
的比值是否发生改变,若不改变求出其比值,若要改变说明理由;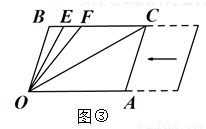


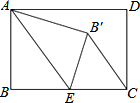 如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C
如图,已知矩形ABCD,点E为BC的中点,将△ABE沿直线AE折叠,点B落在B′点处,连接B′C