题目内容
2.如图,抛物线y=x2-2x-3与x轴交于A、B两点(点A在点B的左边),与y轴交于C点,点D是抛物线的顶点.(1)求B、C、D三点的坐标;
(2)连接BC,BD,CD,若点P为抛物线上一动点,设点P的横坐标为m,当S△PBC=S△BCD时,求m的值(点P不与点D重合);
(3)连接AC,将△AOC沿x轴正方向平移,设移动距离为a,当点A和点B重合时,停止运动,设运动过程中△AOC与△OBC重叠部分的面积为S,请直接写出S与a之间的函数关系式,并写出相应自变量a的取值范围.
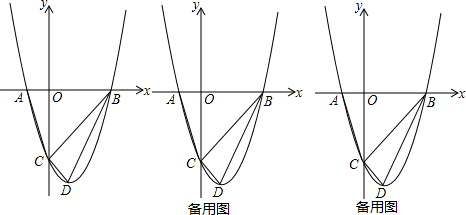
分析 (1)令y=0,解方程即可求得A、B的坐标,令x=0,即可求得C的坐标,把解析式化成顶点式即可求得顶点坐标;
(2)根据待定系数法求得直线BC的解析式,过点D作DE∥y轴,交BC于点E,则xD=1=xE,求得yE=-2,DE=2,进而得出S△BCD=S△BED+S△CDE=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3,然后分两种情况分别讨论求得即可;
(3)分三种情况:①当0<a≤1时,根据S=S△AOC-S△A′OE-S△FGC′即可求得;②当1<a≤3时,如图4,根据S=S△AOC-S△FGC′=即可求得;③当3<a≤4时,如图5,S=$\frac{1}{2}$(4-a)×$\frac{3}{4}$(4-a).
解答 解:(1)当y=0时,x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
当x=0时,y=-3,
∴C(0,-3),
∵y=x2-2x-3=(x-1)2-4,
∴D(1,-4);
(2)设BC:y=kx+b
将B(3,0),C(0,-3)代入得:$\left\{\begin{array}{l}{0=3k+b}\\{-3=b}\end{array}\right.$解得$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$,
∴直线BC为y=x-3,
过点D作DE∥y轴,交BC于点E,
∵xD=1=xE,
∴yE=-2,
∴DE=2,
∴S△BCD=S△BED+S△CDE=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3,
过点P作PQ∥y轴,交直线BC于点Q,设P(m,m2-2m-3),Q(m,m-3)
①当P是BC下方抛物线上一点时,如图1,
∴${S_{△PCB}}={S_{△PBQ}}+{S_{△PQC}}=-\frac{3}{2}{m^2}+\frac{9}{2}m=3$.
∴m1=-1(舍),m2=2,
②当P是BC上方抛物线上一点时,如图2,
S△PBC=S△PQC-S△PQB=$\frac{3}{2}$m2-$\frac{9}{2}$m=3,
解得m1=$\frac{3+\sqrt{17}}{2}$,m2=$\frac{3-\sqrt{17}}{2}$,
综上:m的值为$\frac{{3+\sqrt{17}}}{2},\frac{{3-\sqrt{17}}}{2},2$;
(3) ①当0<a≤1时,如图3,
①当0<a≤1时,如图3,
∵OA′=1-a,O′C′=OC=3,
∵$\frac{AE}{O′C′}$=$\frac{OA′}{O′A′}$
即$\frac{AE}{3}$=$\frac{1-a}{1}$,
∴AE=3-3a,
∴CE=3a,
∵$\frac{O′G}{OC}$=$\frac{O′B}{OB}$,
即$\frac{O′G}{3}$=$\frac{3-a}{3}$,
∴O′G=3-a,
∴GC′=a,
∵$\frac{EC}{C′G}$=$\frac{3a}{a}$=$\frac{3}{1}$,
∴△FC′G边CG′上的高为$\frac{1}{4}$a,
∴S=S△AOC-S△A′OE-S△FGC′=$\frac{1}{2}$×1×3-$\frac{1}{2}$(1-a)×(3-3a)-$\frac{1}{2}$a×$\frac{1}{4}$a=-$\frac{13}{8}$a2+3a;
②当1<a≤3时,如图4,
∵GC=a,△FC′G边CG′上的高为$\frac{1}{4}$a,
∴S=S△AOC-S△FGC′=$\frac{1}{2}$×1×3-$\frac{1}{2}$a×$\frac{1}{4}$a=-$\frac{1}{8}$a2+$\frac{3}{2}$;
③当3<a≤4时,如图5,
∵A′B=4-a,CC′=a, 设△A′FB边A′B上的高为h,则△CFC′边CC′的高为3-h,
设△A′FB边A′B上的高为h,则△CFC′边CC′的高为3-h,
∵△A′FB∽△C′FC,
∴$\frac{h}{3-h}$=$\frac{4-a}{a}$,解得h=$\frac{3}{4}$(4-a),
∴S=$\frac{1}{2}$(4-a)×$\frac{3}{4}$(4-a)=$\frac{3}{8}$a2-3a+6;
综上,$S=\left\{\begin{array}{l}-\frac{13}{8}{a^2}+3a(0<a≤1)\\-\frac{1}{8}{a^2}+\frac{3}{2}(1<a≤3)\\ \frac{3}{8}{a^2}-3a+6(3<a≤4)\end{array}\right.$.
点评 本题是二次函数的综合题,考查了待定系数法求函数的解析式,抛物线的交点坐标,三角形的面积等,分类讨论思想的应用是解题的关键.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | a4m-2a2mb2n+b4m | B. | a4m-b4 | C. | a4m+b4n | D. | a2m+b2n+2ambn |
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 2x-1 | |||||||
| -3x | |||||||
| x2 |
(2)已知有两个x的值使代数式-3x和x2的值相等,你能找出这两个x值吗?
(3)随着x的值的逐渐增大,代数式2x-1、-3x和x2的值是如何变化的?(写出结论即可,无需说明理由)
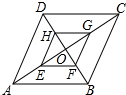 如图,在?ABCD中,对角线AC,BD相交于点O、E、F、G、H分别是OA、OB、OC、OD的中点.
如图,在?ABCD中,对角线AC,BD相交于点O、E、F、G、H分别是OA、OB、OC、OD的中点. 如图,在平面直角坐标系中,一块等腰直角三角形ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y=$\frac{3}{2}$x2+bx+c的图象经过B,C两点,过点C作CD⊥y轴,垂足为点D
如图,在平面直角坐标系中,一块等腰直角三角形ABC的直角顶点A在y轴上,坐标为(0,-1),另一顶点B坐标为(-2,0),已知二次函数y=$\frac{3}{2}$x2+bx+c的图象经过B,C两点,过点C作CD⊥y轴,垂足为点D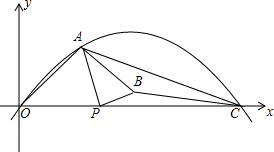 如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC.
如图,抛物线y=ax2+bx+c经过点O(0,0),A(3,4)和C(11,0),点P(t,0)是x轴上的一个动点,以P为圆心,$\frac{1}{2}$AP长为半径,顺时针方向转90°得PB,连AB、BC、AC.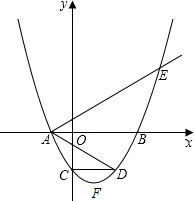 如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE
如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE