题目内容
 如图,平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?说说你的理由.
如图,平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?说说你的理由.考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:利用平行四边形的性质得出AD∥BC,BO=DO,进而得出△DOF≌△BIE(AAS),进而得出答案.
解答:解:相等,
理由:∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AD∥BC,BO=DO,
∴∠ADO=∠BOE,
在△DOF和△BIE中,
,
∴△DOF≌△BIE(AAS),
∴EO=FO.
理由:∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AD∥BC,BO=DO,
∴∠ADO=∠BOE,
在△DOF和△BIE中,
|
∴△DOF≌△BIE(AAS),
∴EO=FO.
点评:此题主要考查了平行四边形的性质以及全等三角形的判定与性质,得出△DOF≌△BIE是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若M的值使得x2+4x+M=(x+2)2-1成立,则M的值为( )
| A、5 | B、4 | C、3 | D、2 |
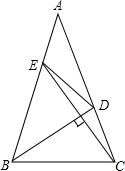 如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )
如图,△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,CE⊥BD交于E,连接DE,则图中等腰三角形有( )| A、3个 | B、4个 | C、5个 | D、6个 |
下列图形中,∠1与∠2互为对顶角的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=2.Rt△AB′C′可以看作是由Rt△ABC绕A点逆时针方向旋转60°得到的,求线段 B′C的长. 小明在某次投篮中,球的运动路线是抛物线y=-
小明在某次投篮中,球的运动路线是抛物线y=- 如图网格中每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的三个顶点均在网格上.
如图网格中每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的三个顶点均在网格上.