题目内容
18.抛物线y=-$\frac{1}{2}$(x+1)2与抛物线y=(x+1)2关于x轴成轴对称; 抛物线y=-$\frac{1}{2}$(x+1)2与抛物线y=-(x-1)2关于y轴成轴对称.分析 由关于x轴对称点的特点是:横坐标不变,纵坐标变为相反数,可求出抛物线y=-(x+1)2-2关于x轴对称的抛物线解析式;再由关于y轴对称点的特点是:纵坐标不变,横坐标变为相反数,可得关于y轴对称的抛物线解析式.
解答 解:∵y=-(x+1)2,
∴关于x轴对称的抛物线解析式为-y=-(x+1)2,即y=(x+1)2;
∴关于y轴对称的抛物线解析式为y=-(-x+1)2,即y=-(x-1)2.
故答案为y=(x+1)2;y=-(x-1)2.
点评 此题考查了二次函数的图象与几何变换,解题的关键是抓住关于x轴、y轴对称点的特点.

练习册系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 任意两个矩形形状相同 | B. | 任意两个菱形形状相同 | ||
| C. | 任意两个直角三角形相似 | D. | 任意两个正五边形形状相同 |
13.若一个圆锥的底面半径为3cm,高为4cm,则这个圆锥的全面积为( )
| A. | 15π cm2 | B. | 24π cm2 | C. | 34π cm2 | D. | 39π cm2 |
8.已知∠a=30°,则∠a的余角的度数为( )
| A. | 60° | B. | 90° | C. | 150° | D. | 180° |
 如图,AB:BC:CD=2:3:4,如果AB中点M和CD中点N的距离是24cm,求AB,ND,MN的长度.
如图,AB:BC:CD=2:3:4,如果AB中点M和CD中点N的距离是24cm,求AB,ND,MN的长度. 圆锥的侧面展开图是扇形,图是三棱柱的表面展开图.
圆锥的侧面展开图是扇形,图是三棱柱的表面展开图. 在街道c上修建一个加油站使它到公路a与公路b的距离相等.
在街道c上修建一个加油站使它到公路a与公路b的距离相等.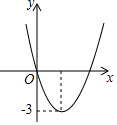 已知:二次函数y=ax2+bx+c的图象如图所示,根据图象可知,当k>3时,关于x的方程|ax2+bx+c|=k有两个不相等的实数根.
已知:二次函数y=ax2+bx+c的图象如图所示,根据图象可知,当k>3时,关于x的方程|ax2+bx+c|=k有两个不相等的实数根.