题目内容
19．设关于x的一元二次方程x2+kx-1=0的两实根分别x1，x2，且满足x1+x2=x2•x2，求k的值．分析 先利用根与系数的关系得到x1+x2=-k，x1x2=-1，则利用x1+x2=x2•x2得到-k=-1，然后解一次方程即可得到k的值．
解答 解：根据题意得x1+x2=-k，x1x2=-1，
∵x1+x2=x2•x2，
∴-k=-1，
∴k=1．
点评 本题考查了根与系数的关系：若：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
9．下列函数中，y是x的二次函数的是（ ）
| A． | y=2x-1 | B． | y=-$\frac{1}{x}$ | C． | y=2x2-3x+1 | D． | y=$\frac{1}{{{x^2}-2}}$ |
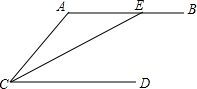如图，已知∠ACE=∠AEC，CE平分∠ACD，则AB∥CD，用推理的方法说明它是一个真命题．
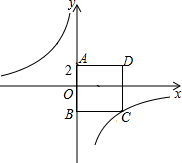如图，四边形ABCD为正方形，点A的坐标为（0，2），点B的坐标为（0，-3），反比例函数y1=$\frac{k}{x}$的图象经过点C，一次函数y2=ax+b的图象经过点A、C．