题目内容
19. 如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )
如图,AC与BD相交于点E,AD∥BC.若AE=2,CE=3,AD=3,则BC的长度是( )| A. | 2 | B. | 3 | C. | 4.5 | D. | 6 |
分析 根据AD∥BC,推出△ADE∽△BCE,根据相似三角形的性质得到$\frac{AE}{CE}=\frac{AD}{BC}$,代入数据即可得到结论.
解答 解:∵AD∥BC,
∴△ADE∽△BCE,
∴$\frac{AE}{CE}=\frac{AD}{BC}$,
即:$\frac{2}{3}=\frac{3}{BC}$,
∴BC=$\frac{9}{2}$,
故选C.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
4.抛物线y=-2x2+3的顶点在( )
| A. | x轴上 | B. | y轴上 | C. | 第一象限 | D. | 第四象限 |
8.某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下(单位:千米):
(1)求收工时检修小组距离A地多远?
(2)第几次纪录时检修小组距离A地最远?
(3)若每千米耗油0.5升,每升汽油需6元,问检修小组工作一天需汽油费多少元?
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
| -3 | +8 | -9 | +10 | +4 | -6 | -2 |
(2)第几次纪录时检修小组距离A地最远?
(3)若每千米耗油0.5升,每升汽油需6元,问检修小组工作一天需汽油费多少元?
9.某商品经过连续两次降价,销售单价由原来100元降到81元.设平均每次降价的百分率为x,根据题意可列方程为( )
| A. | 81(1-x)2=100 | B. | 100(1+x)2=81 | C. | 81(1+x)2=100 | D. | 100(1-x)2=81 |
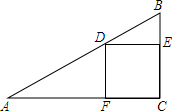 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.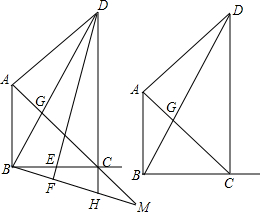
 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.
如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.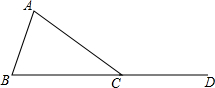 如图,点D在△ABC的BC边的延长线上,且∠A=∠B.
如图,点D在△ABC的BC边的延长线上,且∠A=∠B.