题目内容
 如图,在平面直角坐标系xOy中,二次函数y=-x2+2x+8的图象与一次函数y=-x+b的图象交于A、B两点,点A在x轴上,点B的纵坐标为-7.点P是二次函数图象上A、B两点之间的一个动点(不与点A、B重合),设点P的横坐标为m,过点P作x轴的垂线交AB于点C,作PD⊥AB于点D.
如图,在平面直角坐标系xOy中,二次函数y=-x2+2x+8的图象与一次函数y=-x+b的图象交于A、B两点,点A在x轴上,点B的纵坐标为-7.点P是二次函数图象上A、B两点之间的一个动点(不与点A、B重合),设点P的横坐标为m,过点P作x轴的垂线交AB于点C,作PD⊥AB于点D.(1)求b及sin∠ACP的值;
(2)用含m的代数式表示线段PD的长;
(3)连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m值,使这两个三角形的面积之比为1:2?如果存在,直接写出m的值;如果不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)已知直线AB的解析式,首先能确定A、B点的坐标,然后利用待定系数法确定a、b的值;若设直线AB与y轴的交点为E,E点坐标易知,在Rt△AEO中,能求出sin∠AEO,而∠AEO=∠ACP,则∠ACP的正弦值可得;
(2)已知P点横坐标,根据直线AB、抛物线的解析式,求出C、P的坐标,由此得到线段PC的长;在Rt△PCD中,根据(1)中∠ACP的正弦值,即可求出PD的表达式;
(3)在表达△PCD、△PBC的面积时,若都以PC为底,那么它们的面积比等于PC边上的高的比.分别过B、D作PC的垂线,首先求出这两条垂线段的表达式,然后根据题干给出的面积比例关系求出m的值.
(2)已知P点横坐标,根据直线AB、抛物线的解析式,求出C、P的坐标,由此得到线段PC的长;在Rt△PCD中,根据(1)中∠ACP的正弦值,即可求出PD的表达式;
(3)在表达△PCD、△PBC的面积时,若都以PC为底,那么它们的面积比等于PC边上的高的比.分别过B、D作PC的垂线,首先求出这两条垂线段的表达式,然后根据题干给出的面积比例关系求出m的值.
解答:解:(1)∵当y=0时,-x2+2x+8=0,
∴x1=-2,x2=4∵点A在x轴负半轴上,
∴A(-2,0),OA=2,
∵点A在一次函数y=-x+b的图象上,
∴2+b=0,
∴b=-2,
∴一次函数表达式为y=-x-2,
设直线AB交y轴于点E,则E(0,-2),OE=OA=2,
∵PC⊥x轴交AB于点C,
∴PC∥y轴,
∴∠AEO=∠ACP=45°,
∴sin∠ACP=sin45°=
;
(2)∵点P在二次函数y=-x2+2x+8图象上且横坐标为m,
∴P(m,-m2+2m+8),
∵PC⊥x轴且点C在一次函数y=-x-2的图象上,
∴C(m,-m-2),
∴PC=-m2+3m+10,
∵PD⊥AB于点D,
∴在Rt△CDP中,sin∠ACP=
=
,
∴PD=-
m2+
m+5
;
(3)如图,分别过点D、B作DF⊥PC,BG⊥PC,垂足分别为F、G.
∵sin∠ACP=
,
∴cos∠ACP=
,
又∵∠FDP=∠ACP
∴cos∠FDP=
,
在Rt△PDF中,DF=
PD=-
m2+
m+5,
又∵BG=5-m,
∴当
=
=
时,解得m=-1,
当
=
=2时,解得m=2,
∴m的值为-1和2.
∴x1=-2,x2=4∵点A在x轴负半轴上,
∴A(-2,0),OA=2,
∵点A在一次函数y=-x+b的图象上,
∴2+b=0,
∴b=-2,
∴一次函数表达式为y=-x-2,
设直线AB交y轴于点E,则E(0,-2),OE=OA=2,
∵PC⊥x轴交AB于点C,
∴PC∥y轴,
∴∠AEO=∠ACP=45°,
∴sin∠ACP=sin45°=
| ||
| 2 |
(2)∵点P在二次函数y=-x2+2x+8图象上且横坐标为m,
∴P(m,-m2+2m+8),
∵PC⊥x轴且点C在一次函数y=-x-2的图象上,
∴C(m,-m-2),
∴PC=-m2+3m+10,
∵PD⊥AB于点D,
∴在Rt△CDP中,sin∠ACP=
| PD |
| PC |
| ||
| 2 |
∴PD=-
| ||
| 2 |
3
| ||
| 2 |
| 2 |
(3)如图,分别过点D、B作DF⊥PC,BG⊥PC,垂足分别为F、G.

∵sin∠ACP=
| ||
| 2 |
∴cos∠ACP=
| ||
| 2 |
又∵∠FDP=∠ACP
∴cos∠FDP=
| ||
| 2 |
在Rt△PDF中,DF=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
又∵BG=5-m,
∴当
| S△PCD |
| S△PBC |
| DF |
| BG |
| 1 |
| 2 |
当
| S△PCD |
| S△PBC |
| DF |
| BG |
∴m的值为-1和2.
点评:本题考查了二次函数的应用以及解析式的确定、解直角三角形、图形面积的求法等知识,主要考查学生数形结合思想的应用能力,题目的综合性很强,对学生的解题能力要求很高,是一道不错的中考压轴题.

练习册系列答案
相关题目
 如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠C=60°,BC=4,CD=3,求AB的长.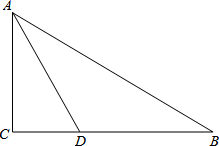 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的平分线. 如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=
如图,AC是⊙O的切线,BC是直径,AB交⊙O于点D,∠A=50°,那么∠COD=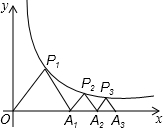 如图,P1、P2、P3…Pn(n为正整数)分别是反比例函数y=
如图,P1、P2、P3…Pn(n为正整数)分别是反比例函数y=