题目内容

6．如图，在等腰三角形纸片ABC中，AB=AC，∠A=46°，折叠该纸片，使点A落在点B处，折痕为DE，则∠CBE=21°．

分析 首先运用等腰三角形的性质求出∠ABC的大小；借助翻折变换的性质求出∠ABE的大小问题即可解决．

解答 解：∵AB=AC，且∠A=46°，
∴∠ABC=∠C=（180°-46°）÷2=67°；
∵翻折，
∴AE=BE，
∴∠A=∠ABE=46°，
∴∠CBE=67°-46°=21°，
故答案为：21．

点评 此题考查了折叠的性质、等腰三角形的性质及三角形内角和定理．掌握折叠前后图形的对应关系，结合图形解决问题．

练习册系列答案
相关题目
16．可能用到的下列运算关系式：
（1）（a+b）（a-b）=a2-b2
（2）${a^{-p}}=\frac{1}{a^p}$
（3）（am）n=amn
已知：f（x）=2x+2-x，g（x）=2x-2-x，例如：当x=3时，$f（3）={2^3}+{2^{-3}}=8\frac{1}{8}$
（1）设F（x）=f（x）×g（x），则F（2）=15$\frac{15}{16}$；
（2）试证明对任意的x值都有：F（x）+F（-x）=0．
17．某商店经销甲、乙两种商品．请您根据图中所给的信息解答下列问题：
（1）求甲、乙两种商品的零售单价；
（2）该商店平均每天卖出甲商品500件和乙商品1000件．经调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件．商店决定把甲种商品的零售单价下降m（m＞0）元．在不考虑其他因素的条件下，当m为多少时，商店每天销售甲、乙两种商品获取的总利润为1500元？
14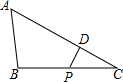．如图，在△ABC中，∠ABC＞90°，∠C=30°，BC=12，P是BC上的一个动点，过点P作PD⊥AC于点D，设CP=x，△CDP的面积为y，则y与x之间的函数图象大致为（　　）
A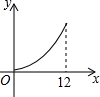．B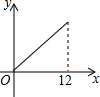．C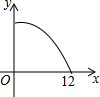．D．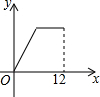
1．有四个命题：
①等弧所对的圆周角相等；
②圆周角相等，相对的弧也相等；
③在同一个圆中，如果弧相等，那么联结弧两端的弦也相等；
④在同一个圆中，如果弦相等，那么以弦的两端为端点的弧也相等．
其中错误的是（　　）
A．1个B．2个C．3个D．4个
11．一个口袋中有红、白、黑球共10个，这些球除颜色外都相同，将口袋中的球搅拌均匀，从中随机摸出一个球，记下颜色后放回袋中．不断重复这个过程，共摸了100次球，发现有49次摸到红球，21次摸到黑球，则袋中白球大约是（　　）
A．5个B．4个C．3个D．2个
18．方程x（x+1）=3（x+1）的根是x1=-1，x2=3．
15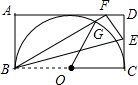．如图，在矩形ABCD中，BC=12，以BC为直径的半圆O恰好与AD相切，现将矩形ABCD沿BE折叠，使点C落在边AD的点F处，并交半圆O于点G，则扇形OCG的面积为（　　）
A．6πB．12πC．24πD．无法确定
16．已知⊙O的半径是一元二次方程x2-6x+9=0的解，且点O到直线AB的距离为2，则⊙O与直线AB的位置关系为（　　）
A．相交B．相切C．相离D．无法确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网