题目内容
2.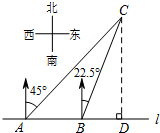 如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km.
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为(2+$\sqrt{2}$)km.
分析 根据题意在CD上取一点E,使BD=DE,进而得出EC=BE=2km,再利用勾股定理得出DE的长,即可得出答案.
解答  解:在CD上取一点E,使BD=DE,
解:在CD上取一点E,使BD=DE,
∵CD⊥AB,
∴∠EBD=45°,AD=DC,
∵AB=AD-BD,CE=CD-DE,
∴CE=AB=2km,
∵从B测得船C在北偏东22.5°的方向,
∴∠BCE=∠CBE=22.5°,
∴BE=EC=2km,
∴BD=ED=$\sqrt{2}$km,
∴CD=2+$\sqrt{2}$(km).
故答案为:(2+$\sqrt{2}$)km.
点评 此题考查了方向角问题.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
14.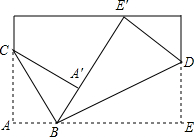 同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
 同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
同学们,你玩过折纸游戏吗?折纸游戏里还蕴藏着不少数学知识呢!请准备一张长方形纸片,按照小亮的方法折纸,折叠后A′B与E′B在同一直线上,如图所示,则两折痕BC与BD的夹角∠CBD的度数为90°.
5. 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )
 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )
如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为点D,则AD的长为( )| A. | $\frac{25}{4}$ | B. | 6 | C. | $\frac{24}{5}$ | D. | 4 |
 △ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).
△ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-2).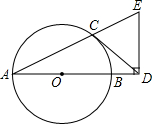 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.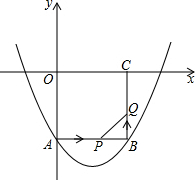 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-$\frac{2}{3}$).
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B和D(4,-$\frac{2}{3}$).