题目内容
观察下列等式:
?1×3+1=22
?3×5+1=42
?5×7+1=62
…
(1)请你按照上述三个等式的规律写出第④个、第⑤个等式;
(2)请猜想,第n个等式(n为正整数)应表示为 ;
(3)证明你猜想的结论.
?1×3+1=22
?3×5+1=42
?5×7+1=62
…
(1)请你按照上述三个等式的规律写出第④个、第⑤个等式;
(2)请猜想,第n个等式(n为正整数)应表示为
(3)证明你猜想的结论.
考点:规律型:数字的变化类
专题:
分析:(1)根据数字的变化规律,可知左边为连续两个奇数的积与1的和,右边为这两个奇数中间的偶数的平方,可得出答案;
(2)根据(1)的规律可写出答案;
(3)把左边用整式的乘法计算出其结果,与右边相等,可证得结论.
(2)根据(1)的规律可写出答案;
(3)把左边用整式的乘法计算出其结果,与右边相等,可证得结论.
解答:解:(1)第④个算式为:7×9+1=82,
第⑤个算式为:9×11+1=102;
(2)第n个算式为:(2n-1)(2n+1)+1=(2n)2;
故答案为:(2n-1)(2n+1)+1=(2n)2;
(3)证明:∵左边=(2n-1)(2n+1)+1=4n2+1-1=4n2,
右边=(2n)2=4n2,
∴(2n-1)(2n+1)+1=(2n)2.
第⑤个算式为:9×11+1=102;
(2)第n个算式为:(2n-1)(2n+1)+1=(2n)2;
故答案为:(2n-1)(2n+1)+1=(2n)2;
(3)证明:∵左边=(2n-1)(2n+1)+1=4n2+1-1=4n2,
右边=(2n)2=4n2,
∴(2n-1)(2n+1)+1=(2n)2.
点评:本题主要考查数字的变化规律,通过观察得出“左边为连续两个奇数的积与1的和,右边为这两个奇数中间的偶数的平方”是解题的关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、1.45°=87′ |
| B、1800″=30° |
| C、当时钟指向3:30时,时针与分钟的夹角是90° |
| D、两个锐角的和一定是钝角 |
 如图,直线y=-2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过A点分别作两坐标轴的垂线,垂足分别为B、C.
如图,直线y=-2x+8与两坐标轴分别交于P、Q两点,在线段PQ上有一点A,过A点分别作两坐标轴的垂线,垂足分别为B、C. 如图,直线y=kx+b与坐标轴的两个交点分别为A(2,0),B(0,-3),则不等式kx+b+3≥0的解为
如图,直线y=kx+b与坐标轴的两个交点分别为A(2,0),B(0,-3),则不等式kx+b+3≥0的解为
 如图,在△ABC中,AD平分∠BAC,DE∥AC,EF∥BC,若AB=15,AF=4,则DE=
如图,在△ABC中,AD平分∠BAC,DE∥AC,EF∥BC,若AB=15,AF=4,则DE=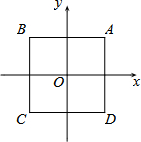 如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.写出一个函数y=x2+c,使它的图象与正方形ABCD有公共点,这个函数的表达式为
如图,在平面直角坐标系xOy中,点O是边长为2的正方形ABCD的中心.写出一个函数y=x2+c,使它的图象与正方形ABCD有公共点,这个函数的表达式为