题目内容
12．已知a，b满足方程组$\left\{\begin{array}{l}{a+2b=3-m}\\{2a+b=-m+4}\end{array}\right.$，则a-b的值为（ ）| A． | -1 | B． | m-1 | C． | 0 | D． | 1 |
分析 方程组两方程相减表示出a-b即可．
解答 解：$\left\{\begin{array}{l}{a+2b=3-m①}\\{2a+b=-m+4②}\end{array}\right.$，
②-①得：a-b=1，
故选D
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
名校课堂系列答案
相关题目
2．
实数a、b在数轴上的对应的位置如图所示，则正确的结论是（ ）
实数a、b在数轴上的对应的位置如图所示，则正确的结论是（ ）| A． | b＞-1 | B． | b＜-2 | C． | a＞-b | D． | a＜-b |
3．
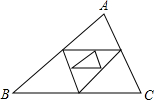如下图，已知△ABC周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边中点构成第三个三角形，依此类推，第2017个三角形周长为（ ）
如下图，已知△ABC周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边中点构成第三个三角形，依此类推，第2017个三角形周长为（ ）| A． | $\frac{1}{2016}$ | B． | $\frac{1}{2017}$ | C． | $\frac{1}{{2}^{2016}}$ | D． | $\frac{1}{{2}^{2017}}$ |
20．计算（3a-2b）2的结果为（ ）
| A． | 9a2+4b2 | B． | 9a2+6ab+4b2 | C． | 9a2-12ab+4b2 | D． | 9a2-4b2 |
7．下列四个实数中，最小的是（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | $\sqrt{3}$ | D． | 1.4 |
17．
如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB=40°，点D是弧BAC上一点，连结CD．则∠D的度数是（ ）
如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB=40°，点D是弧BAC上一点，连结CD．则∠D的度数是（ ）| A． | 50° | B． | 45° | C． | 40° | D． | 35° |
4．
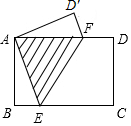如图，矩形纸片ABCD中，AB=3cm，现将纸片折叠压平，使点A与点C重合，折痕为EF，如果sin∠BAE=$\frac{5}{13}$，那么重叠部分△AEF的面积为（ ）
如图，矩形纸片ABCD中，AB=3cm，现将纸片折叠压平，使点A与点C重合，折痕为EF，如果sin∠BAE=$\frac{5}{13}$，那么重叠部分△AEF的面积为（ ）| A． | $\frac{39}{4}$ | B． | $\frac{39}{8}$ | C． | $\frac{15}{4}$ | D． | $\frac{15}{8}$ |
1．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
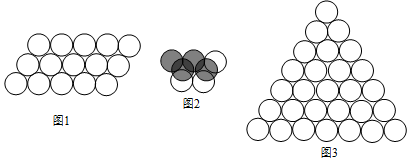
10．五一假期，小明和小华共同设计了一款拼图，他们用乒乓球粘成了下面几种造型的拼板（每种一块，没有重复）：
（1）你能用部分拼板拼成图1中的平行四边形吗？所使用的拼板形状不能重复，请在图1中用不同颜色或底纹画出来．
（2）如图2，小华想用拼板摆出一个三棱锥造型，三棱锥的每条棱上有三个乒乓球，他已经用A5和B完成了一部分（图2是从上往下看的样子），请从剩下的拼板中挑出一块完成拼图，你认为需要的拼板是A1．
（3）小明试图用部分拼板拼出图3中的大三角形，请判断他能否成功？如果能，在图3中用不同颜色或底纹画出拼板的摆法；如果不能，请说明理由．
| A组 |  |  |  | |||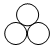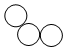
| A1 | A2 | A3 | ||||
| B组 |  |  |  |  |  |  |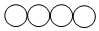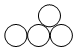
| B1 | B2 | B3 | B4 | B5 | B6 |
（2）如图2，小华想用拼板摆出一个三棱锥造型，三棱锥的每条棱上有三个乒乓球，他已经用A5和B完成了一部分（图2是从上往下看的样子），请从剩下的拼板中挑出一块完成拼图，你认为需要的拼板是A1．
（3）小明试图用部分拼板拼出图3中的大三角形，请判断他能否成功？如果能，在图3中用不同颜色或底纹画出拼板的摆法；如果不能，请说明理由．