题目内容
20.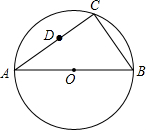 如图,AB为⊙O的直径,点C为⊙O上一动点,点D为弦AC的中点.
如图,AB为⊙O的直径,点C为⊙O上一动点,点D为弦AC的中点.(1)当$\widehat{AC}$=2$\widehat{BC}$,求∠BAC的度数;
(2)若AB=4,当点C在⊙O上运动时,点D始终在一个圆上,请你确定这个圆的圆心以及这个圆的半径.
分析 (1)由AB为⊙O的直径,根据直径所对的圆周角是直角,可得∠C=90°,由$\widehat{AC}$=2$\widehat{BC}$,可得∠B=2∠A,继而求得答案;
(2)首先连接OD,由点D为弦AC的中点,易得OD是△ABC的中位线,继而可得∠ADO=90°,即可知点D在以OA为直径的圆上,则可求得答案.
解答 解:(1)∵AB为⊙O的直径,
∴∠C=90°,
∴∠A+∠B=90°,
∵$\widehat{AC}$=2$\widehat{BC}$,
∴∠B=2∠A,
∴3∠A=90°,
解得:∠BAC=30°; (2)连接OD,
(2)连接OD,
∵OA=OB,点D为弦AC的中点,
∴OD∥BC,
∴∠ADO=∠C=90°,
∴点D在以OA为直径的圆上,
∵AB=4,
∴OA=2,
∴圆心是:OA的中点,这个圆的半径为:1.
点评 此题考查了圆周角定理以及三角形中位线的性质.注意准确作出辅助线,确定点D在以OA为直径的圆上是解此题的关键.

练习册系列答案
相关题目
14. 如图,等边三角形ABC内接于⊙O,点P在$\widehat{AB}$上,则∠BPC等于( )
如图,等边三角形ABC内接于⊙O,点P在$\widehat{AB}$上,则∠BPC等于( )
 如图,等边三角形ABC内接于⊙O,点P在$\widehat{AB}$上,则∠BPC等于( )
如图,等边三角形ABC内接于⊙O,点P在$\widehat{AB}$上,则∠BPC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.下列各组长度的线段能构成三角形的是( )
| A. | 1.5cm,3.9cm,2.3cm | B. | 3.5cm,7.1cm,3.6cm | ||
| C. | 6cm,1cm,6cm | D. | 4cm,10cm,4cm |

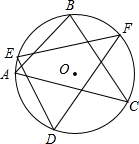 已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.
已知,如图,在⊙O中,AB=DE,BC=EF.求证:AC=DF.