题目内容
9.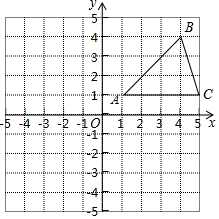 在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).(1)若△ABC和△A1B1C1关于原点O成中心对称图形,画出△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
(3)在x轴上存在一点P,满足点P到点B1与点C1距离之和最小,请直接写出P B1+P C1的最小值为$\sqrt{34}$.
分析 (1)根据关于原点中心对称的点的坐标特征写出点A1、B1、C1的坐标,从而得到△A1B1C1;
(2)利用网格特点和旋转的性质画出点B、C的对应点B2、C2,从而得到△AB2C2;
(3)作C1点关于x轴的对称点C′,连接B1C′交x轴于P点,则PC1=PC′,则P B1+P C1=P B1+P C′=B1C′,利用两点之间线段最短可得到此时P B1+P C1的值最小值,然后利用勾股定理计算出B1C′即可.
解答 解:(1)如图,△A1B1C1所作;
(2)如图,△AB2C2为所作;
(3)作C1点关于x轴的对称点C′,连接B1C′交x轴于P点,
则PC1=PC′,P B1+P C1=P B1+P C′=B1C′=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
所以P B1+P C1的最小值为$\sqrt{34}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
14. 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )| A. | 32 | B. | 36 | C. | 40 | D. | 56 |
19.把多项式m2-9m分解因式,结果正确的是( )
| A. | m(m-9) | B. | (m+3)(m-3) | C. | m(m+3)(m-3) | D. | (m-3)2 |
 如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008).
如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…、则正方形OB2016B2017C2017的顶点B2017的坐标是(21008,21008).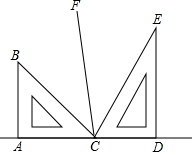 把两个三角尺按如图所示那样拼在一起(三角尺分别含30°,45°,60°,90°角,点A、C、D在一条直线上).
把两个三角尺按如图所示那样拼在一起(三角尺分别含30°,45°,60°,90°角,点A、C、D在一条直线上).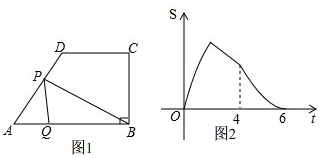 如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.
如图,已知四边形ABCD中,AB∥CD,∠ABC=90°,AB=2CD,点P从点A出发以每秒2个单位沿折线AD-DC-CB运动,同时点Q从点A出发以每秒1个单位向点B运动,当其中一个点到达终点时,另一个点也停止运动,连结PQ、PB,设△PBQ的面积为S,运动时间为t秒,S关于t的大致函数图象如图所示.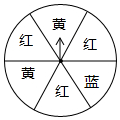 转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次)
转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次)