题目内容
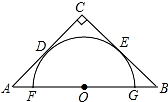 如图,半圆O与等腰直角三角形ABC的两腰CA、CB分别切于D、E两点,直径FG在AB上,若BG=
如图,半圆O与等腰直角三角形ABC的两腰CA、CB分别切于D、E两点,直径FG在AB上,若BG=| 2 |
考点:切线的性质,等腰直角三角形
专题:
分析:首先连接OD,OE,易证得四边形ODCE是正方形,△OEB是等腰直角三角形,首先设OE=r,由OB=
OE=
r,可得方程:
-1+r=
r,解此方程,即可求得答案
| 2 |
| 2 |
| 2 |
| 2 |
解答:
解:连接OD,OE,
∵半圆O与等腰直角三角形两腰CA、CB分别切于D、E两点,
∴∠C=∠OEB=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形,
∴CD=CE=OE,
∵∠A=∠B=45°,
∴∠EOB=∠EBO=45°,
∴OE=EB,
∴△OEB是等腰直角三角形,
设OE=r,
∴BE=OE=OG=r,
∴OB=OG+BG=
-1+r,
∵OB=
OE=
r,
∴
-1+r=
r,
∴r=1,
∴BE=1.
故答案为1.

∵半圆O与等腰直角三角形两腰CA、CB分别切于D、E两点,
∴∠C=∠OEB=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵OD=OE,
∴四边形ODCE是正方形,
∴CD=CE=OE,
∵∠A=∠B=45°,
∴∠EOB=∠EBO=45°,
∴OE=EB,
∴△OEB是等腰直角三角形,
设OE=r,
∴BE=OE=OG=r,
∴OB=OG+BG=
| 2 |
∵OB=
| 2 |
| 2 |
∴
| 2 |
| 2 |
∴r=1,
∴BE=1.
故答案为1.
点评:此题考查了切线的性质、正方形的判定与性质以及等腰直角三角形的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x=3是一元二次方程x2+mx+3=0的一个解,则m的值是( )
| A、4 | B、-4 | C、0 | D、0或4 |
下列各组数中,互为相反数的是( )
A、-3和
| ||||
| B、|-3|和-(-3) | ||||
| C、3和-3 | ||||
D、
|
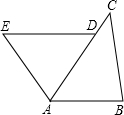 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,线段BC和AE相等吗?为什么?
如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,线段BC和AE相等吗?为什么?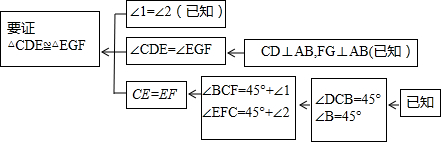
 已知点P在△AOB内,点M,N分别是点P关于射线OA,OB的对称点,点M,N的连线与OA,OB交于点E、F,若MN的长为20cm,求△PEF的周长.
已知点P在△AOB内,点M,N分别是点P关于射线OA,OB的对称点,点M,N的连线与OA,OB交于点E、F,若MN的长为20cm,求△PEF的周长.