题目内容
已知x=3是一元二次方程x2+mx+3=0的一个解，则m的值是（ ）
| A、4 | B、-4 | C、0 | D、0或4 |
考点：一元二次方程的解
专题：
分析：根据一元二次方程的解的定义，将x=3代入已知方程列出关于m的新方程，通过解新方程即可求得m的值．
解答：
解：∵x=3是一元二次方程x2+mx+3=0的一个解，
∴x=3满足一元二次方程x2+mx+3=0，
∴32+3m+3=0，即3m+12=0，
解得，m=-4；
故选B．
∴x=3满足一元二次方程x2+mx+3=0，
∴32+3m+3=0，即3m+12=0，
解得，m=-4；
故选B．
点评：本题考查的是一元二次方程的根即方程的解的定义．一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
如图所示，已知DE∥BC，CD平分∠ACB，∠ACB=120°，∠B=30°．请探究直线CD与AB的位置关系，并说明理由．小明家冰箱冷冻室的温度为-5℃，调低4℃后的温度为（ ）
| A、-9℃ | B、4℃ |
| C、-1℃ | D、9℃ |
在线段、等边三角形、平行四边形、矩形、菱形、正方形、等腰梯形中，既是中心对称图形又是轴对称图形的有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
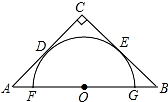如图，半圆O与等腰直角三角形ABC的两腰CA、CB分别切于D、E两点，直径FG在AB上，若BG=