题目内容
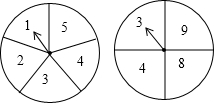 你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,
你喜欢转盘游戏吗?如图,图中的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,(1)请用列表法或树形图分析指针都落在奇数上的概率是多少?
(2)甲、乙两人约定:若转到的数字点数之和为奇数,则甲胜;反之,则乙胜.你认为这个游戏是否公平?说明你的理由.
考点:游戏公平性,列表法与树状图法
专题:
分析:(1)列举出所有情况,看转盘停止后,指针都落在奇数上的情况数占总情况数的多少即可.
(2)游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等即可.
(2)游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等即可.
解答:
解:(1)列表可得
共20种可能的结果,它们出现的可能性相同,其中都是奇数有6种情况,
∴P(都是奇数)=
=
;
(2)由表可知:P(甲胜)=
(1分)P(乙胜)=
(1分),
∴P(甲胜)=P(乙胜),
∴游戏公平.
| 3 | 4 | 8 | 9 | |
| 1 | √ | √ | ||
| 2 | ||||
| 3 | √ | √ | ||
| 4 | ||||
| 5 | √ | √ |
∴P(都是奇数)=
| 6 |
| 20 |
| 3 |
| 10 |
(2)由表可知:P(甲胜)=
| 1 |
| 2 |
| 1 |
| 2 |
∴P(甲胜)=P(乙胜),
∴游戏公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知一次函数y=kx+b的图象经过一、二、四象限,则下列判断正确的是( )
| A、k>0,b>0 |
| B、k<0,b<0 |
| C、k>0,b<0 |
| D、k<0,b>0 |
点(-2,-5)所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
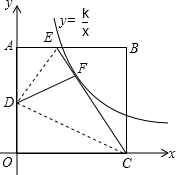 如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=
如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=