题目内容
12.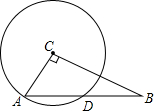 已知:如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,
已知:如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,(1)求AD的长;
(2)若∠B=28°,求弧$\widehat{AD}$的度数;
(3)若点P是线段AB上的动点,则线段CP的长度取值范围是$\frac{18}{5}$≤CP≤4.
分析 (1)先根据勾股定理求出AB的长,过C作CM⊥AB,交AB于点M,由垂径定理可知M为AD的中点,由三角形的面积可求出CM的长,在Rt△ACM中,根据勾股定理可求出AM的长,进而可得出结论;
(2)根据等腰三角形的性质和三角形的内角和得到∠ACD=34°,于是得到结论;
(3)根据题意即可得到结论.
解答 解:∵在Rt△ABC中,∠ACB=90°,AC=3,BC=4,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
过C作CM⊥AB,交AB于点M,如图所示,
∵CM⊥AB,
∴M为AD的中点,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM,且AC=3,BC=4,AB=5,
∴CM=$\frac{12}{5}$,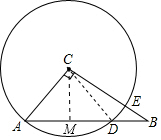
在Rt△ACM中,根据勾股定理得:AC2=AM2+CM2,即9=AM2+($\frac{12}{5}$)2,
解得:AM=$\frac{9}{5}$,
∴AD=2AM=$\frac{18}{5}$;
(2)∵∠ACB=90°,∠B=28°,
∴∠A=62°,
连接CD,
∵AC=CD,
∴∠CDA=∠A=28°,
∴∠ACD=34°,
∴弧$\widehat{AD}$的度数是34°;
(3)线段CP的长度取值范围是$\frac{18}{5}$≤CP≤4.
故答案为:$\frac{18}{5}$≤CP≤4.
点评 本题考查的是垂径定理,等腰三角形的性质,三角形的内角和,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.二次函数y=x2-2x-6的对称轴为( )
| A. | x=2 | B. | x=-2 | C. | x=1 | D. | x=-1 |
3.(1)特例导航:请依据所给的运算程序完成填空.
(2)探索与归纳:如果把你最初提供的那个任意三位数用n表示,请将上述运算所含的规律,用一个含有n的等式表示出来:$\frac{1001n}{7×11×13}$=n
并通过计算说明这个等式的正确性.
| 运算程序 | 例如 | 按左侧的形式完成你的举例 |
| ①给出任意一个三位数 | 325 | 123 |
| ②重复①中的数,得到一个新的数字 | 325325 | 123123 |
| ③将②的结果除以7 | 325325÷7=a46475 | 123123÷7=17589 |
| ④将③的结果除以11 | a÷11=b4225 | 17589÷11=1599 |
| ⑤将④的结果除以13 | b÷13=325 | 1599÷13=123 |
并通过计算说明这个等式的正确性.
7. 如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
 如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )
如图,点A、D、G、M在半圆O上,四边形ABOC、DEOF、HMNO均为矩形,设BC=a,EF=b,NH=c,则下列各式中正确的是( )| A. | a>b>c | B. | a=b=c | C. | c>a>b | D. | b>c>a |
4.某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时,其它主要参考数据如下:
(1)如果A市与某市之间的距离为400千米,根据上面的表格你可以算出:
选择火车运输的总费用是8800,选择汽车运输的总费用是9900.
(2)如果选择汽车的总费用比选择火车费用多1100元,那么本市与A市之间的路程是多少千米?
| 运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
| 火车 | 100 | 15 | 2000 |
| 汽车 | 80 | 20 | 900 |
选择火车运输的总费用是8800,选择汽车运输的总费用是9900.
(2)如果选择汽车的总费用比选择火车费用多1100元,那么本市与A市之间的路程是多少千米?
1.下列说法正确的是( )
| A. | 单项式$\frac{1}{2}$xy的系数是$\frac{1}{2}$,次数是1 | |
| B. | 单项式-$\frac{1}{3}$πa2b3的系数是-$\frac{1}{3}$,次数是6 | |
| C. | 单项式x2的系数是1,次数是2 | |
| D. | 多项式2x3-3x2y2+x-1叫三次四项式 |