题目内容
4.已知二次函数y=x2+bx+c的图象经过一次函数y=-3x+3的图象与x轴、y轴的交点.求这个二次函数解析式,并直接回答该函数有最小值(最大值或最小值)为-1.分析 首先求得y=-3x+3与x轴、y轴的交点坐标,利用待定系数法求得二次函数的解析式,然后求得最值.
解答 解:在y=-3x+3中令x=0,则y=3,则y=-3x+3与y轴的交点是(0,3);
在y=-3x+3中,令y=0,则-3x+3=0,解得x=1,则与x轴的交点是(1,0);
根据题意得:$\left\{\begin{array}{l}{c=3}\\{1+b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-4}\\{c=3}\end{array}\right.$,
则二次函数的解析式是y=x2-4x+3=(x-2)2-1.
则函数有最小值是-1.
故答案是:小,-1.
点评 本题考查了待定系数法求函数的解析式以及函数图象与x轴、y轴交点的求法,求与x轴交点时令y=0求得横坐标,求与y轴的交点时令x=0求纵坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在一个不透明的袋中,装有3个红球和1个白球,这些球除颜色外其余都相同,搅匀后从中随机一次摸出两个球,这两个球都是红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
12.判断$\sqrt{11}×\sqrt{30}$的值会介于下列哪两个整数之间( )
| A. | 17,18 | B. | 18,19 | C. | 19,20 | D. | 21,22 |
19.估计$\sqrt{7}$的值在( )
| A. | 0和1之间 | B. | 1和2之间 | C. | 2和3之间 | D. | 3和4之间 |
14.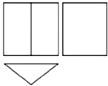 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )
 一个几何体的三视图如图所示,那么这个几何体是( )
一个几何体的三视图如图所示,那么这个几何体是( )| A. | 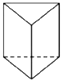 | B. | 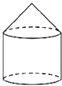 | C. | 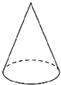 | D. |  |
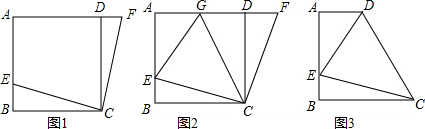
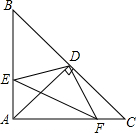 如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,连接AD,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.
如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,连接AD,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5. 形状相同、大小相等的两个小木块放置于桌面,其俯视图如图所示,则其左视图是( )
形状相同、大小相等的两个小木块放置于桌面,其俯视图如图所示,则其左视图是( )


