题目内容
20.化简:(1)(π-2016)0+$\sqrt{21}+|{\sqrt{3}-3}$|
(2)$\sqrt{16}+\root{3}{-27}-\sqrt{{{({-3})}^2}}+{({-\frac{1}{2}})^{-2}}$
(3)3$\sqrt{20}-\sqrt{45}-4\sqrt{\frac{1}{5}}$
(4)$\frac{{\sqrt{2}×\sqrt{6}}}{{\sqrt{8}}}-\sqrt{\frac{50}{3}}+\sqrt{27}÷\sqrt{8}$
(5)$({1+\sqrt{3}})({\sqrt{2}-\sqrt{6}})-{({2\sqrt{3}-1})^2}$.
分析 根据实数的运算的法则,零指数幂的性质,负整数幂的性质,二次根式的化简计算即可.
解答 解:(1)(π-2016)0+$\sqrt{21}+|{\sqrt{3}-3}$|=1+$\sqrt{21}$+3-$\sqrt{3}$=4+$\sqrt{21}$-$\sqrt{3}$;
(2)$\sqrt{16}+\root{3}{-27}-\sqrt{{{({-3})}^2}}+{({-\frac{1}{2}})^{-2}}$=4-3-3+4=4-6=2;
(3)3$\sqrt{20}-\sqrt{45}-4\sqrt{\frac{1}{5}}$=2$\sqrt{5}$-3$\sqrt{5}$-$\frac{4\sqrt{5}}{5}$=-$\frac{9\sqrt{5}}{5}$;
(4)$\frac{{\sqrt{2}×\sqrt{6}}}{{\sqrt{8}}}-\sqrt{\frac{50}{3}}+\sqrt{27}÷\sqrt{8}$=$\frac{\sqrt{3}}{2}$-$\frac{5\sqrt{6}}{3}$+$\frac{3\sqrt{6}}{2}$=$\frac{3\sqrt{3}-\sqrt{6}}{6}$;
(5)$({1+\sqrt{3}})({\sqrt{2}-\sqrt{6}})-{({2\sqrt{3}-1})^2}$=$\sqrt{2}$-3$\sqrt{2}$-13+4$\sqrt{3}$=4$\sqrt{3}$-2$\sqrt{2}$-13.
点评 本题考查了实数的运算的法则,零指数幂的性质,负整数幂的性质,二次根式的化简,熟记法则是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.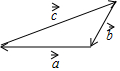 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )
 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,那么下列结论正确的是( )| A. | $\overrightarrow{a}$$+\overrightarrow{b}$=$\overrightarrow{c}$ | B. | $\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{a}$ | C. | $\overrightarrow{a}$$+\overrightarrow{c}$=$\overrightarrow{b}$ | D. | $\overrightarrow{a}$$+\overrightarrow{c}$=$-\overrightarrow{b}$ |
8.小明的文具袋里有一塑料的等腰直角三角板,教师的讲台上有一木制的大的等腰直角三角板,那么这两个三角板( )
| A. | 无法比较 | B. | 边长不成比例 | C. | 不相似 | D. | 相似 |
9.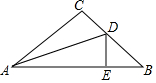 如图,Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB,若CD=5cm,则BE的长为( )
如图,Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB,若CD=5cm,则BE的长为( )
 如图,Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB,若CD=5cm,则BE的长为( )
如图,Rt△ABC中,∠C=90°,AC=BC,AD平分∠CAB,DE⊥AB,若CD=5cm,则BE的长为( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
 如图,已知∠AOB=60°,点P在边OA上,OP=24,点M,N在边OB上,PM=PN,若NM=6,则OM等于( )
如图,已知∠AOB=60°,点P在边OA上,OP=24,点M,N在边OB上,PM=PN,若NM=6,则OM等于( )