��Ŀ����
��ͼ��AC�ǡ�O��ֱ����BC�ǡ�O���ң���P�ǡ�O��һ�㣬����PB��AB����PBA=��C��
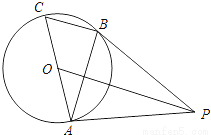
��1����֤��PB�ǡ�O�����ߣ�
��2������OP����OP��BC����OP=8����O�İ뾶Ϊ2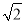 ����BC�ij���
����BC�ij���
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��AC�ǡ�O��ֱ����BC�ǡ�O���ң���P�ǡ�O��һ�㣬����PB��AB����PBA=��C��

��1����֤��PB�ǡ�O�����ߣ�
��2������OP����OP��BC����OP=8����O�İ뾶Ϊ2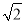 ����BC�ij���
����BC�ij���