题目内容
16.若不等式组$\left\{\begin{array}{l}{2x-1<1}\\{x+1>a}\end{array}\right.$恰有两个整数解,则a的取值范围是( )| A. | -1≤a<0 | B. | -1<a≤0 | C. | -1≤a≤0 | D. | -1<a<0 |
分析 首先解不等式组求得不等式组的解集,然后根据不等式组有两个整数解即可确定整数解,从而得到关于a的不等式,求得a的范围.
解答 解:$\left\{\begin{array}{l}{2x-1<1…①}\\{x+1<a…②}\end{array}\right.$,
解①得x<1,
解②得x>a-1,
则不等式组的解集是a-1<x<1.
又∵不等式组有两个整数解,
∴整数解是0,-1.
∴-2≤a-1-<-1,
解得:-1≤a<0.
故选A.
点评 本题考查了不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
相关题目
11.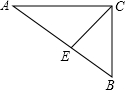 如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
 如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )
如图,在△ABC中,CE是角平分线,∠ACB=90°,若∠A=35°,则∠CEB的度数为( )| A. | 70° | B. | 75° | C. | 80° | D. | 90° |
 已知,在正方形ABCD中,点G、F在AD上,E为AB的中点,CG⊥EF于点H,若AD=4AG,BH=$\frac{8}{5}\sqrt{5}$,则DH=$\frac{4}{5}$$\sqrt{10}$.
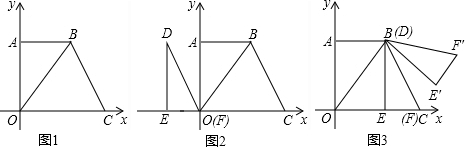
已知,在正方形ABCD中,点G、F在AD上,E为AB的中点,CG⊥EF于点H,若AD=4AG,BH=$\frac{8}{5}\sqrt{5}$,则DH=$\frac{4}{5}$$\sqrt{10}$. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是$\frac{27}{2}$,S3的值为$\frac{{3}^{8}}{{2}^{5}}$.
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=$\frac{1}{2}$x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则第4个正方形的边长是$\frac{27}{2}$,S3的值为$\frac{{3}^{8}}{{2}^{5}}$. 如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),在第一象限内,画出以原点为位似中心,与原四边形ABCD相似比为$\frac{1}{2}$的位似图形A1B1C1D1,并写出各点坐标.
如图,四边形ABCD各顶点的坐标分别为A(2,6),B(4,2),C(6,2),D(6,4),在第一象限内,画出以原点为位似中心,与原四边形ABCD相似比为$\frac{1}{2}$的位似图形A1B1C1D1,并写出各点坐标.