题目内容
8．可以用3个同样大小的正六边形地砖围绕一点铺成平整、无缝隙的平面．可以用3个边长相等的正三角形与两个同样边长的正方形地砖围绕一点铺成平整、无缝隙的平面．分析 绕一点铺成平整、无缝隙的平面，则组成周角为360°，所以让一个点组成的角的和为360°即可．
解答 解：因为正六边形的每一个内角为：180°-$\frac{360}{6}$=120°，
且360°÷120°=3，
所以可以用3个同样大小的正六边形地砖围绕一点铺成平整、无缝隙的平面；
两个同样边长的正方形的每个角为90°，则两个正方形的角的和为180°，
一个正三角形的内角为60°，
所以需要3个正三角形与两个同样边长的正方形地砖围绕一点铺成平整、无缝隙的平面；
故答案为：3，3．
点评 本题考查了平面镶嵌，判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能．
练习册系列答案
相关题目
11．一元二次方程x2-16=0的根是（ ）
| A． | x=2 | B． | x=4 | C． | x1=2，x2=-2 | D． | x1=4，x2=-4 |
16．若不等式组$\left\{\begin{array}{l}{2x-1＜1}\\{x+1＞a}\end{array}\right.$恰有两个整数解，则a的取值范围是（ ）
| A． | -1≤a＜0 | B． | -1＜a≤0 | C． | -1≤a≤0 | D． | -1＜a＜0 |
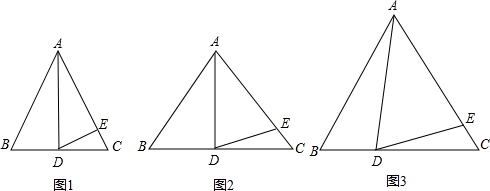
如图，AD是△ABC的角平分线，BE是△ABC的高，∠BAC=40°，则∠AFE的度数为70°．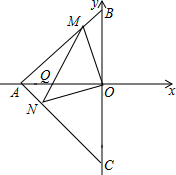
已知A（-4，0），B（0，4），C（0，-4），过O作OM⊥ON交AB、AC于M、N两点