题目内容
 如图,点A(m,2),B(n,2)分别是反比例函数y=-
如图,点A(m,2),B(n,2)分别是反比例函数y=-| 4 |
| x |
| 2 |
| x |
考点:轴对称-最短路线问题,反比例函数图象上点的坐标特征
专题:
分析:作A关于x轴的对称点C,连接BC,交x轴于P,则P即为使PA+PB有最小值的点,根据轴对称的性质求得C的坐标,然后求得BC即可.
解答:解:∵点A(m,2),B(n,2)分别是反比例函数y=-
,y=
在x轴上方的图象上的点,
∴2=-
,解得m=-2,
2=
,解得n=1,
∴A(-2,2),B(1,2),
作A关于x轴的对称点C,连接BC,交x轴于P,则P即为使PA+PB有最小值的点,此时PA+PB=BC;

∴C(-2,-2),
∴BC=
=5;
∴PA+PB的最小值为5;
故答案为5.
| 4 |
| x |
| 2 |
| x |
∴2=-
| 4 |
| m |
2=
| 2 |
| n |
∴A(-2,2),B(1,2),
作A关于x轴的对称点C,连接BC,交x轴于P,则P即为使PA+PB有最小值的点,此时PA+PB=BC;

∴C(-2,-2),
∴BC=
| (1+2)2+(2+2)2 |
∴PA+PB的最小值为5;
故答案为5.
点评:本题考查了反比例函数图象上点的坐标特征,轴对称-最短路线问题,勾股定理的应用等,熟练掌握轴对称的性质是解题的关键.

练习册系列答案
相关题目
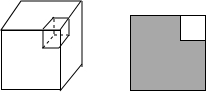 如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )
如图所示,在边长为a的正方形中减去一个边长为b的小正方形(a>b),剩下的部分的面积,可得到平方差公式;那么在边长a的正方体中减去一个边长为b的小正方体(a>b),剩下的部分的体积为a3-b3,它等于( )| A、(a+b)(a2-ab+b2) |
| B、(a-b)(a2+ab+b2) |
| C、(a-b)(a2+b2) |
| D、(a+b)(a2-b2) |
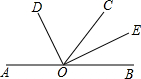 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.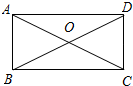 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积. 如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.
如图,在△ABC中有矩形DGFE,点G,F在BC上,点D,E分别在AB,AC上,AH⊥BC交DE于点M.若DG:DE=2:3,BC=15cm,AH=10cm,求矩形DGFE各边的长.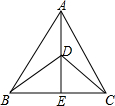 已知,如图,在△ABC中,BD=DC,∠ADB=∠ADC.求证:∠ABC=∠ACB.
已知,如图,在△ABC中,BD=DC,∠ADB=∠ADC.求证:∠ABC=∠ACB.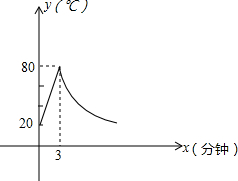 制作一种模型,需要先将材料加热,待其充分融合后,再进行操作.该材料的温度为y(℃),从加热开始计算的时间为x(分钟).该材料加热时,温度y与x成一次函数关系,停止加热后,温度y与x成反比例函数关系.如图,已知该材料在加热前的温度为20℃,加热3分钟后温度达到80℃.
制作一种模型,需要先将材料加热,待其充分融合后,再进行操作.该材料的温度为y(℃),从加热开始计算的时间为x(分钟).该材料加热时,温度y与x成一次函数关系,停止加热后,温度y与x成反比例函数关系.如图,已知该材料在加热前的温度为20℃,加热3分钟后温度达到80℃.