题目内容
10.(1)计算:6×3-1-(2015-π)0+$\sqrt{8}$×$\sqrt{2}$;(2)先化简,再求值:($\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$)÷$\frac{x}{x-1}$,其中x=$\sqrt{2}$+1.
分析 (1)分别根据0指数幂、负整数指数幂的计算法则、数的开方法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原式=6×$\frac{1}{3}$-1+4
=2-1+4
=5;
(2)原式=($\frac{x}{x-1}$+$\frac{1}{(x-1)^{2}}$)÷$\frac{x}{x-1}$
=$\frac{{x}^{2}}{{(x-1)}^{2}}$•$\frac{x-1}{x}$
=$\frac{x}{x-1}$,
当x=$\sqrt{2}$+1时,原式=$\frac{\sqrt{2}+1}{\sqrt{2}+1-1}$=$\frac{\sqrt{2}+1}{\sqrt{2}}$=$\frac{2+\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
18. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )
 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )
如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90°,OA与反比例函数y=$\frac{k}{x}$的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )| A. | -16 | B. | 16 | C. | -15 | D. | 15 |
5.下列说法中正确的是( )
| A. | 一个抽奖活动的中奖率是5%,则抽100次奖一定会中奖5次 | |
| B. | 了解某批炮弹的杀伤半径,采取普查方式 | |
| C. | 一组数据1、2、3、4的中位数是2.5 | |
| D. | 若甲组数据的方差是S甲2=0.1,乙组数据的方差是S乙2=0.01,则甲组数据比乙组数据稳定 |
2.某同学抽取20名学生统计某月的用笔数量情况,结果如下表:
则关于这20名学生这个月的用笔数量的描述,下列说法正确的是( )
| 用笔数(支) | 4 | 5 | 6 | 8 | 9 |
| 学生数 | 4 | 4 | 7 | 3 | 2 |
| A. | 众数是7支 | B. | 中位数是6 | C. | 平均数是5支 | D. | 方差为0 |
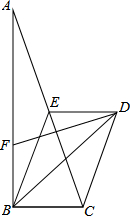 如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.求证:
如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.求证: 如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.
如图,生活中都把自行车的几根梁做成三角形的支架,这是因为三角形具有稳定性.