题目内容
20.甲、乙两辆车同时从A地出发沿着一条笔直的公路匀速前往B地,A、B两地之间的路程为120千米,甲、乙两车的速度之比为3:2,结果甲车比乙车早到了$\frac{2}{3}$小时.(1)求甲、乙两车每小时分别行驶多少千米?
(2)甲车到达B地后不停留,直接按原来速度返回A地,乙车到达B地后停留一段时间也按原速度返回.若当甲车回到A地时,乙车至少要驶离B地20千米,那么乙车在B地停留最多不超过多少小时?
分析 (1)设甲每小时分别行驶3x千米,乙每小时分别行驶2x千米,依据“甲车比乙车早到了$\frac{2}{3}$小时”列出方程并解答,注意:分式方程需要验根;
(2)设乙车在B地停留a小时,根据已知条件列出不等式并解答.
解答 解:(1)设甲每小时分别行驶3x千米,乙每小时分别行驶2x千米,$\frac{120}{3x}$=$\frac{120}{2x}$-$\frac{2}{3}$.
解得:x=30.
经检验,x=30是原方程的解.
则3x=90,2x=60.
答:设甲每小时分别行驶90千米,乙每小时分别行驶60千米;
(2)设乙车在B地停留a小时,则
120×2÷90=$\frac{8}{3}$(小时),
($\frac{8}{3}$-a)×60≥120+20,
解得:a≤$\frac{1}{3}$.
答:乙车在B地停留最多不能超过$\frac{1}{3}$小时.
点评 本题考查了一元一次不等式的应用,分式方程的应用.利用分式方程解应用题时,一般题目中会有两个相等关系,这时要根据题目所要解决的问题,选择其中的一个相等关系作为列方程的依据,而另一个则用来设未知数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在Rt△ABC中,∠C=90°,∠A=15°,AB的垂直平分线和AC相交于点M,则CM:MA等于( )
| A. | 1:$\sqrt{3}$ | B. | $\sqrt{3}:1$ | C. | 2:$\sqrt{3}$ | D. | $\sqrt{3}:2$ |
15.下列计算正确的是( )
| A. | a3•a2=a6 | B. | (3+a)2=9+a2 | C. | 3a-4a=-a | D. | (-a2)3=a6 |
9.下列运算正确的是( )
| A. | x2+x4=x6 | B. | x6÷x3=x2 | ||
| C. | $\frac{-a-b}{a+b}$=-1 | D. | $\frac{b}{{a}^{2}-{b}^{2}}$÷(1-$\frac{a}{a+b}$)=-$\frac{1}{a-b}$ |
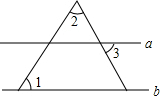 如图,a∥b,∠1=55°,∠2=65°,则∠3的大小为60°.
如图,a∥b,∠1=55°,∠2=65°,则∠3的大小为60°. 如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )
如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )


