题目内容
11. 如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=25°,则∠2的度数为70°.
如图,a∥b,点A在直线a上,点C在直线b上,∠BAC=90°,AB=AC,若∠1=25°,则∠2的度数为70°.
分析 先根据等腰三角形的性质求出∠ACB的度数,再由平行线的性质即可得出结论.
解答 解:∵∠BAC=90°,AB=AC,
∴∠ACB=∠B=45°.
∵∠1=25°,
∴∠1+∠ACB=70°.
∵a∥b,
∴∠2=∠1+∠ACB=70°.
故答案为:70°
点评 本题考查的是等腰三角形的性质,熟知等腰三角形的两个底角相等是解答此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
2.一个两位数,个位数字为a,十位数字为b,则这个两位数为( )
| A. | 10b+a | B. | ba | C. | 10a+b | D. | ab |
1.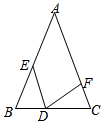 如图,在△ABC中,AB=AC,BD=CF,BE=CD,若∠A=40°,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,BD=CF,BE=CD,若∠A=40°,则∠EDF的度数为( )
 如图,在△ABC中,AB=AC,BD=CF,BE=CD,若∠A=40°,则∠EDF的度数为( )
如图,在△ABC中,AB=AC,BD=CF,BE=CD,若∠A=40°,则∠EDF的度数为( )| A. | 75° | B. | 70° | C. | 65° | D. | 60° |
 如图,已知∠1=∠2,AC=AD,有下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC∽△AED的条件有 ( )
如图,已知∠1=∠2,AC=AD,有下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC∽△AED的条件有 ( )