题目内容
如图,已知△ABC中,AB=AC=6,BC=8,点D是BC边上的一个动点,点E在AC边上,∠ADE=∠B.设BD的长为x,CE的长为y.
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.
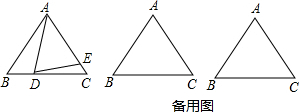
(1)当D为BC的中点时,求CE的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADE为等腰三角形,求x的值.

考点:相似三角形的判定与性质,等腰三角形的性质,直角三角形斜边上的中线,勾股定理
专题:
分析:(1)先根据等腰三角形的性质由AB=AC得∠B=∠C,再利用三角形外角性质得∠ADC=∠ADE+∠CDE=∠B+∠BAD,加上∠ADE=∠B,则∠BAD=∠CDE,根据相似三角形的判定方法待定△ABD∽△DCE,利用相似比得到y=-
x2+
x(0≤x≤8),然后把x=4代入计算得到CE的长为
;
(2)由(1)得到y关于x的函数关系式为y=-
x2+
x(0≤x≤8);
(3)由于∠AED>∠C,而∠B=∠ADE=∠C,则∠AED>∠ADE,所以AE<AD,然后分类讨论:当DA=DE时,利用△ABD∽△DCE得到
=1,即x=y,得到一元二次方程-
x2+
x=x,解方程得x1=0,x2=2;当EA=ED时,得到∠EAD=∠ADE,而∠ADE=∠C,所以∠EAD=∠C,可判断△DAC∽△ABC,利用相似比得到
=
,解得x=
.
| 1 |
| 6 |
| 4 |
| 3 |
| 8 |
| 3 |
(2)由(1)得到y关于x的函数关系式为y=-
| 1 |
| 6 |
| 4 |
| 3 |
(3)由于∠AED>∠C,而∠B=∠ADE=∠C,则∠AED>∠ADE,所以AE<AD,然后分类讨论:当DA=DE时,利用△ABD∽△DCE得到
| x |
| y |
| 1 |
| 6 |
| 4 |
| 3 |
| 8-x |
| 6 |
| 6 |
| 8 |
| 7 |
| 2 |
解答:解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,
而∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴
=
,
=
,
∴y=-
x2+
x,
当x=4时,y=-
×16+
×4=
,
即当D为BC的中点时,CE的长为
;
(2)由(1)得y关于x的函数关系式为y=-
x2+
x(0≤x≤8);
(3)∵∠AED>∠C,
而∠B=∠ADE=∠C,
∴∠AED>∠ADE,
∴AE<AD,
当DA=DE时,
∵△ABD∽△DCE,
∴
=
,即
=1,
∴x=y,
∴-
x2+
x=x,解得x1=0,x2=2,
当EA=ED时,则∠EAD=∠ADE,
而∠ADE=∠C,
∴∠EAD=∠C,
∴△DAC∽△ABC,
∴
=
,即
=
,
∴x=
,
综上所述,当△ADE为等腰三角形,x的值为0或2或
.
∴∠B=∠C,
∵∠ADC=∠ADE+∠CDE=∠B+∠BAD,
而∠ADE=∠B,
∴∠BAD=∠CDE,
∴△ABD∽△DCE,
∴
| AB |
| CD |
| BD |
| CE |
| 6 |
| 8-x |
| x |
| y |
∴y=-
| 1 |
| 6 |
| 4 |
| 3 |
当x=4时,y=-
| 1 |
| 6 |
| 4 |
| 3 |
| 8 |
| 3 |
即当D为BC的中点时,CE的长为
| 8 |
| 3 |
(2)由(1)得y关于x的函数关系式为y=-
| 1 |
| 6 |
| 4 |
| 3 |
(3)∵∠AED>∠C,
而∠B=∠ADE=∠C,
∴∠AED>∠ADE,
∴AE<AD,
当DA=DE时,
∵△ABD∽△DCE,
∴
| AD |
| DE |
| BD |
| CE |
| x |
| y |
∴x=y,
∴-
| 1 |
| 6 |
| 4 |
| 3 |
当EA=ED时,则∠EAD=∠ADE,
而∠ADE=∠C,
∴∠EAD=∠C,
∴△DAC∽△ABC,
∴
| DC |
| AB |
| AC |
| BC |
| 8-x |
| 6 |
| 6 |
| 8 |
∴x=
| 7 |
| 2 |
综上所述,当△ADE为等腰三角形,x的值为0或2或
| 7 |
| 2 |
点评:本题考查了相似三角形的判定与性质:平行于三角形一边的直线与其他两边所截的三角形与原三角形相似;相似三角形对应边的比相等,都等于相似比.也考查了等腰三角形的性质.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,在平行四边形ABCD中,E为DC的中点,AE交BD于点F,S△DEF=12cm2,则S△AOB的值为( )
如图,在平行四边形ABCD中,E为DC的中点,AE交BD于点F,S△DEF=12cm2,则S△AOB的值为( )| A、12cm2 |
| B、24cm2 |
| C、36cm2 |
| D、48cm2 |
 如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线,则这块草地的绿地面积为( )
如图,在一块长为a m,宽为b m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线,则这块草地的绿地面积为( )| A、(a-1)b |
| B、a(b-1) |
| C、ab-1 |
| D、(a-1)(b-1) |
 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图的统计图.若该校共有800名学生,估计喜欢“踢毽子”的学生有( )人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图的统计图.若该校共有800名学生,估计喜欢“踢毽子”的学生有( )人.| A、100 | B、200 |
| C、300 | D、400 |
 如图,在边长为1的网格中作出三角形ABC向左移3格,再向下移4格后的三角形A′B′C′.
如图,在边长为1的网格中作出三角形ABC向左移3格,再向下移4格后的三角形A′B′C′.
 已知四边形ABCD外接⊙O的半径为10,对角线AC与BD的交点为E,且AB2=AE•AC,BD=16.
已知四边形ABCD外接⊙O的半径为10,对角线AC与BD的交点为E,且AB2=AE•AC,BD=16.