题目内容
14. 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm.
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm.
分析 先根据等腰梯形ABCD中,AD∥BC,AE∥DC得出四边形AECD是平行四边形,故AE=CD,AD=CE,再由AB=CD可知AB=AE,由∠AEB=60°可知△ABE是等边三角形,故AB=AE=BE=2,再由AD=AB=2即可得出结论.
解答 解:∵等腰梯形ABCD中,AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∴AE=CD,AD=CE.
∵AB=CD,
∴AB=AE.
∵∠AEB=60°,
∴△ABE是等边三角形,
∴AB=AE=BE=2cm.
∵AD=AB=2cm,
∴BC=BE+CE=4cm,
∴梯形ABCD的周长=AB+AD+CD+BC=2+2+2+4=10(cm).
故答案为:10.
点评 本题考查的是等腰梯形的性质,熟知平行四边形及等边三角形的判定定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知反比例函数的图象经过点M(-1,-4),则这个函数的图象位于( )
| A. | 第一、三象限 | B. | 第二、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
3.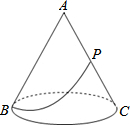 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )| A. | 5m | B. | $3\sqrt{5}$m | C. | 6m | D. | $2\sqrt{5}$m |

 如图,∠MDF=∠EBN,∠A=∠C.
如图,∠MDF=∠EBN,∠A=∠C.



 如图,用一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=-8.
如图,用一个正方体纸盒的展开图,按虚线折成正方体后,相对面上的两个数互为相反数,则ca+b=-8. 如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.
如图所示,直线l1∥l2,AB⊥D于点E,如果∠1=34°,求∠2的度数.