题目内容
3.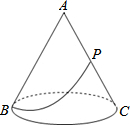 如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )
如图,有一圆锥形粮仓,其正视图为边长是4m的正△ABC,粮仓母线AC的中点P处有一老鼠正在偷吃粮食.此时,小猫正在点B处,它要沿圆锥侧面到达点P处捕捉老鼠,则小猫经过的最短路程为( )| A. | 5m | B. | $3\sqrt{5}$m | C. | 6m | D. | $2\sqrt{5}$m |
分析 求这只小猫经过的最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.根据圆锥的轴截面是边长为4m的等边三角形可知,展开图是半径是4的半圆.点B是半圆的一个端点,而点P是平分半圆的半径的中点,根据勾股定理就可求出两点B和P在展开图中的距离,就是这只小猫经过的最短距离.
解答 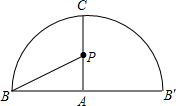 解:∵有一圆锥形粮仓,其正视图为边长是4m的正△ABC,
解:∵有一圆锥形粮仓,其正视图为边长是4m的正△ABC,
∴圆锥的底面周长是4π,则4π=$\frac{nπ×4}{180}$,
∴n=180°,即圆锥侧面展开图的圆心角是180°.
则在圆锥侧面展开图中AP=2,AB=4,∠BAP=90°.
∴在圆锥侧面展开图中BP=$\sqrt{{AB}^{2}+{AP}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$m.
故小猫经过的最短距离是2$\sqrt{5}$m.
故选D.
点评 本题考查的是平面展开-最短路线问题,根据题意画出圆锥的侧面展开图,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
8.如果海平面以上300米记作+300你,则海平面以下11000米记作( )
| A. | -11000米 | B. | +11000米 | ||
| C. | 可能是-11000米也可能是+11000米 | D. | 以上都不对 |
15.在时刻9:30,时钟上时针和分针之间的夹角(小于平角的角)为( )
| A. | 95° | B. | 105° | C. | 110° | D. | 115° |
13. 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
 如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )
如图,若在象棋盘上建立直角坐标系,使“帅”位于点(-1,-2),则“兵”位于点( )| A. | (-3,1) | B. | (-2,-1) | C. | (-1,1) | D. | (1,-2) |
 如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm.
如图,等腰梯形ABCD中,AD∥BC,AE∥DC,∠AEB=60°,AB=AD=2cm,则梯形ABCD的周长为10cm.
 已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF.
已知:如图,E,F是?ABCD的对角线AC上的点,∠ABE=∠CDF.求证:AE=CF.