题目内容
5．若（x2+mx+n）（x-3）的乘积中不含x2和x的项，求m、n的值．分析 根据多项式与多项式的乘法法则展开，再利用不含的项系数等于0列式即可求出m、n的值．
解答 解：（x-3）（x2+mx+n）
=x3+mx2+nx-3x2-3mx-3n
=x3+（m-3）x2+（n-3m）x-3n，
∵不含x2项和x项，
∴m-3=0，n-3m=0，
解得m=3，n=9．
点评 本题主要考查多项式的乘法，运用不含某一项就是该项的系数等于0是解本题的关键，熟练掌握运算法则也很重要．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．
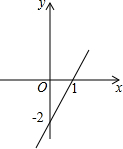如图，已知一次函数y=kx+b（k、b为常数，k≠0）的图象，当y＞-2时，x的取值范围为（ ）
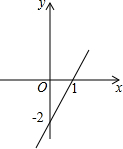如图，已知一次函数y=kx+b（k、b为常数，k≠0）的图象，当y＞-2时，x的取值范围为（ ）| A． | x＜1 | B． | x＞1 | C． | x＜0 | D． | x＞0 |
10．M是线段AB的中点，P是MB上一点，PM等于（ ）
| A． | $\frac{1}{2}$（AM+PB） | B． | $\frac{1}{2}$（PA-PB） | C． | $\frac{1}{2}$AB-PB | D． | 以上都不对 |
如图，在边长为12$\sqrt{2}$的正方形ABCD中，E是AB边上一点，G是AD延长线上一点，BE=DG，连接EG，CF⊥EG交EG于H，交AD于F点，连接CE，BH．若BH=16，则FG=10$\sqrt{2}$．