题目内容
19.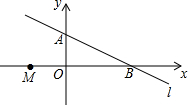 如图,直线l:y=-$\frac{1}{2}$x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,则m的值为2-2$\sqrt{5}$或2+2$\sqrt{5}$..
如图,直线l:y=-$\frac{1}{2}$x+1与坐标轴交于A,B两点,点M(m,0)是x轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线l相切时,则m的值为2-2$\sqrt{5}$或2+2$\sqrt{5}$..
分析 根据直线l:y=-$\frac{1}{2}$x+1由x轴的交点坐标A(0,1),B(2,0),得到OA=1,OB=2,求出AB=$\sqrt{5}$;设⊙M与AB相切与C,连接MC,则MC=2,MC⊥AB,通过△BMC∽△ABO,即可得到结果.
解答  解:在y=-$\frac{1}{2}$x+1中,
解:在y=-$\frac{1}{2}$x+1中,
令x=0,则y=1,
令y=0,则x=2,
∴A(0,1),B(2,0),
∴AB=$\sqrt{5}$;
如图,设⊙M与AB相切与C,
连接MC,则MC=2,MC⊥AB,
∵∠MCB=∠AOB=90°,∠B=∠B,
∴△BMC~△ABO,
∴$\frac{CM}{OA}=\frac{BM}{AB}$,即$\frac{2}{1}=\frac{BM}{\sqrt{5}}$,
∴BM=2$\sqrt{5}$,
∴OM=2$\sqrt{5}$-2,或OM=2$\sqrt{5}$+2.
∴m=2-2$\sqrt{5}$或m=2+2$\sqrt{5}$.
故答案为:2-2$\sqrt{5}$,2+2$\sqrt{5}$.
点评 本题考查了直线与圆的位置关系,一次函数的性质,相似三角形的判定和性质,注意分类讨论是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )| A. | 2$\sqrt{5}$ | B. | 3$\sqrt{5}$ | C. | 5 | D. | 6 |
7.运动会上,某班级买了两种矿泉水,其中甲种矿泉水共花费40元,乙种矿泉水共花费30元.甲种矿泉水比乙种矿泉水多买20瓶,且乙种矿泉水的价格是甲种矿泉水价格的1.5倍.若设甲种矿泉水价格为x元/瓶,根据题意可列方程为( )
| A. | $\frac{40}{1.5x}-\frac{30}{x}$=20 | B. | $\frac{40}{x}-\frac{30}{1.5x}$=20 | C. | $\frac{30}{x}-\frac{40}{1.5x}$=20 | D. | $\frac{30}{1.5x}-\frac{40}{x}$=20 |
9.数5的算术平方根为( )
| A. | $\sqrt{5}$ | B. | 25 | C. | ±25 | D. | ±$\sqrt{5}$ |
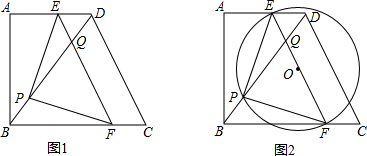
 如图,MN为⊙O直径,A、B是⊙O上,过A作AC⊥MN于C点,过B作BD⊥MN于D点,MN=20,AC=8,BD=6,若点P在直径MN上,则PA+PB最小值是14$\sqrt{2}$.
如图,MN为⊙O直径,A、B是⊙O上,过A作AC⊥MN于C点,过B作BD⊥MN于D点,MN=20,AC=8,BD=6,若点P在直径MN上,则PA+PB最小值是14$\sqrt{2}$.