题目内容
已知x2+x-1=0,则x3+2x2+2011= .
考点:因式分解的应用
专题:
分析:此题运用的是替代法,通过x2+x-1=0,原式可化为x(x2+x-1)+x2+x+2011,据此即可求得代数式的值.
解答:解:∵x2+x-1=0,
∴x3+2x2+2011
=x(x2+x-1)+x2+x+2011
=x2+x-1+2012
=0+2012
=2012.
故答案为:2012.
∴x3+2x2+2011
=x(x2+x-1)+x2+x+2011
=x2+x-1+2012
=0+2012
=2012.
故答案为:2012.
点评:此题考查的是对代数式的替代的运用,根据代数式之间的转化可以求出需要的元素.

练习册系列答案
相关题目
如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
| ||||
| E、? | ||||
| F、? |
点A的坐标是(1,1),若点B在坐标轴上,且△ABO是等腰三角形,则点B的坐标不可能是( )
| A、(2,0) |
| B、(0.5,0) |
| C、(1,0) |
| D、(0,1) |
方程
+
+
+
+
=18的解是( )
| x-2 |
| 3 |
| x-3 |
| 5 |
| x-2 |
| 7 |
| x-5 |
| 9 |
| x-1 |
| 11 |
| A、x=-32 | B、x=32 |
| C、x=-23 | D、x=23 |
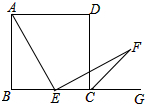 如图,正方形ABCD中,E是BC上的一点,CF为外角的平分线,AE=EF,求证:AE⊥EF.
如图,正方形ABCD中,E是BC上的一点,CF为外角的平分线,AE=EF,求证:AE⊥EF.