题目内容
7.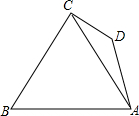 四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长.
四边形ABCD中,BC⊥CD,∠BCA=60°,∠CDA=135°,BC=10.S△ABC=20$\sqrt{3}$.求AD边的长.
分析 作AF⊥AC于F,作AE⊥CD交CD的延长线于E,利用三角形的面积公式S△ABC=$\frac{1}{2}$BC•AF和锐角三角函数的概念求解.
解答 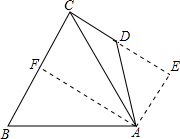 解:作AF⊥BC于F,作AE⊥CD交CD的延长线于E.
解:作AF⊥BC于F,作AE⊥CD交CD的延长线于E.
∵S△ABC=$\frac{1}{2}$BC•AF=$\frac{1}{2}$×10×AF=20$\sqrt{3}$,
∴AF=4$\sqrt{3}$,
∵sin∠BCA=sin60°=AF:AC=$\frac{\sqrt{3}}{2}$,
∴AC=8.
∵BC⊥CD,AE⊥CD
∴∠CAE=∠BCA=60°,
∴∠ACD=90°-60°=30°,
∵∠CDA=135°,
∴AE=ED=sin∠ACD•AC=4.
在等腰直角三角形中AD=$\sqrt{2}$AE=4$\sqrt{2}$.
点评 本题考查了解直角三角形,等腰直角三角形的性质,三角形的面积公式,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
16.南博会的举办将直接提升昆明城市形象及城市核心竞争力.据昆明国际会展中心公布的统计显示:仅6月份的南博会和国际会展两个展会的门票收入,已逾1.2千万.1.2千万这个数用科学记数法应该表示为( )
| A. | 1.2×107 | B. | 1.2×108 | C. | 12×107 | D. | 12×108 |
16.九年级二班50名同学在“爱心捐款”活动中,捐款情况统计如表,
(1)表中a=7;
(2)二班同学捐款数组成的数据中,中位数是12.5、众数是10;
(3)九年级二班50名同学平均捐款多少元?
(4)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
| 捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
| 捐款人数(人) | a | 18 | 10 | 12 | 3 |
(2)二班同学捐款数组成的数据中,中位数是12.5、众数是10;
(3)九年级二班50名同学平均捐款多少元?
(4)根据样本数据,估计该校九年级300名学生在本次活动中捐款多于15元的人数.
17.关于抛物线y=x2和y=-x2,下列说法正确的是( )
| A. | 对称轴都是x轴 | B. | 最低点都是原点(0,0) | ||
| C. | 在y轴右侧呈下降趋势 | D. | 形状相同,开口方向相反 |
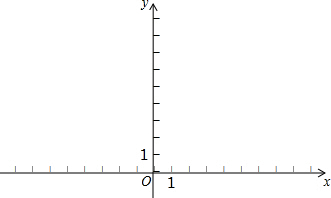
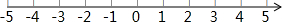 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.