题目内容
4.(1)计算:2sin45°-$\sqrt{8}$+|-2|-(3-π)0(2)先化简后求值:$\frac{4{a}^{2}}{2a-b}$+$\frac{{b}^{2}}{b-2a}$,其中a=1000,b=15.
分析 (1)分别根据特殊角的三角函数值、数的开方法则、绝对值的性质及0指数幂的运算法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把a,b的值代入进行计算即可.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$-2$\sqrt{2}$+2-1
=$\sqrt{2}$-2$\sqrt{2}$+2-1
=1+$\sqrt{2}$;
(2)原式=$\frac{4{a}^{2}}{2a-b}$-$\frac{{b}^{2}}{2a-b}$
=$\frac{4{a}^{2}-{b}^{2}}{2a-b}$
=2a+b.
当a=1000,b=15时,原式=2×1000+15=2015.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.函数y=$\frac{1}{x-3}$中,自变量x的取值范围是( )
| A. | x>3 | B. | x<3 | C. | x=3 | D. | x≠3 |
12.-3的倒数是( )
| A. | 3 | B. | -3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |




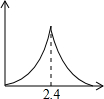
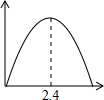
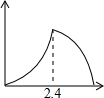
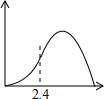
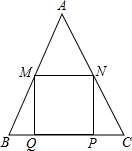 如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y,则y与x的函数图象大致是( )