Question

【题目】内接于⊙，是直径，，点在⊙上.

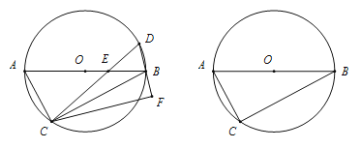
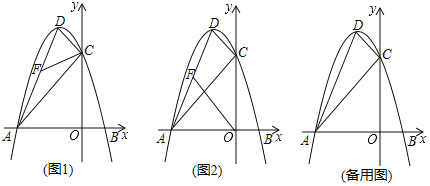
(1)如图，若弦交直径于点，连接，线段是点到的垂线.

①问的度数和点的位置有关吗？请说明理由.

②若的面积是的面积的倍，求的正弦值.

(2)若⊙的半径长为，求的长度.

Answer 1

【答案】（1）没有关系，∠CDF=∠CAB=60°；（2）；（3）或

【解析】

（1）①根据同弧所对的圆周角解答即可；②利用锐角三角函数的定义求出AC与BC、DF与CF的关系，利用三角形的面积公式得出，然后根据正弦的定义可求出的正弦值；

（2）分两种情况求解：①当D点在直径AB下方的圆弧上时；当D点在直径AB上方的圆弧上时.

解：（1）①没有关系，理由如下：

当D在直径AB的上方时，如下图，

∵AB为直径，∴∠ACB=90°；

∵∠ABC=30°，∴∠CAB=60°；

∴∠CDF=∠CAB=60°；

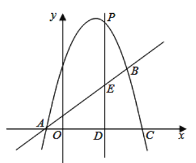
当D在直径AB的下方时，如下图

∵∠CAB=60°，

∴∠CDB=180°-∠CAB=120°,

∴∠CDF=60°.

②∵CF⊥BD，AB为直径；∴ ∠ACB=∠CFD=90°；

由①得，∠CDF=∠CAB=60°，

∴ ；；

∵；；

∴；∴

（2）∵半径为2，，

∴弧CD所对圆心角

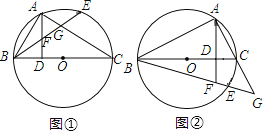
①当D点在直径AB下方的圆弧上时；

如图，连结OD，过D作DE⊥AB于E；

由（1）知，，∴；

∴；

OD=2，∴，，；

∴；

②当D点在直径AB上方的圆弧上时，

如图，连结OD，过D作DF⊥AB于F；

此时；

∴，，；

∴；

综上所述：BD的长为或.