题目内容
阅读理【解析】
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则原方程化为y2﹣5y+4=0,解此方程得:y1=1,y2=4.
当y=1时,x2﹣1═1,∴x=±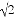 .
.
当y=4时,x2﹣1═4,∴x=±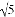 .
.
∴原方程的解为:x1=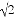 ,x2=﹣
,x2=﹣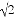 ,x3=
,x3=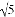 ,x4=﹣
,x4=﹣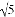 .
.
以上方法叫做换元法解方程,达到了降次的目的,体现了转化思想.
运用上述方法解方程:x4﹣8x2+12=0.
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目