题目内容
20.(1)计算:$|{-\sqrt{3}}|$+$\sqrt{2}$sin45°+tan60°(2)解方程:x2-4x=96.
分析 (1)直接利用特殊角的三角函数值以及绝对值的性质化简求出答案;
(2)直接利用十字相乘法分解因式得出答案.
解答 解:(1)$|{-\sqrt{3}}|$+$\sqrt{2}$sin45°+tan60°
=$\sqrt{3}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$+$\sqrt{3}$
=$1+2\sqrt{3}$;
(2)x2-4x=96
x2-4x-96=0
(x-12)(x+8)=0,
解得:x1=12,x2=-8.
点评 此题主要考查了实数运算以及因式分解法解方程,正确根据相关知识化简各数是解题关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
8.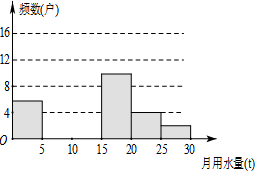 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
请解答以下问题:
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | n |
| 60≤x<70 | 2 | 0.04 |
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
15.下列叙述正确的是( )
| A. | 方差越大,说明数据就越稳定 | |
| B. | 一元二次方程x2-x+1=0有两个不相等的实数根 | |
| C. | 圆内接四边形对角互补 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
 如图,AB是⊙O的直径,C是⊙O上的一点,∠CAE=∠B,你认为AE与⊙O相切吗?为什么?
如图,AB是⊙O的直径,C是⊙O上的一点,∠CAE=∠B,你认为AE与⊙O相切吗?为什么? 如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,
如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,