题目内容
2.已知:一元二次方程$\frac{1}{2}$x2+kx+k-$\frac{1}{2}$=0.(1)对于任意实数k,判断方程的根的情况,并说明理由
(2)设k<0,当二次函数y=$\frac{1}{2}$x2+kx+k-$\frac{1}{2}$的图象与x轴的两个交点A、B间的距离为4时,求k的值.
分析 (1)根据函数与方程的关系,求出△的值,根据△的数值判定解的情况.
(2)根据二次函数图象与x轴的两个交点的距离公式解答即可.
解答 解:(1)方程总有两个实数根;
∵△=k2-4×$\frac{1}{2}$×(k-$\frac{1}{2}$)=k2-2k+1=(k-1)2≥0,
∴关于x的一元二次方程$\frac{1}{2}$x2+kx+k-$\frac{1}{2}$=0.,不论k为何实数时,此方程总有两个实数根;
(2)令y=0,则x2+2kx+2k-1=0.
∵xA+xB=-2k,xA•xB=2k-1,
∴|xA-xB|=$\sqrt{({x}_{A}+{x}_{B})^{2}-4{x}_{A}{x}_{B}}$=$\sqrt{4{k}^{2}-8k+4}$=2|k-1|=4,即|k-1|=2,
解得k=3(不合题意,舍去),或k=-1.
∴k=-1.
点评 本题主要考查了二次函数与方程的联系,抛物线与x轴的交点坐标以及根的判别式的运用,灵活利用两点之间的距离公式解决问题.

练习册系列答案
相关题目
7.下列说法不正确的是( )
| A. | 0的平方根是0 | |
| B. | -22的平方根是±2 | |
| C. | 非负数的平方根是互为相反数 | |
| D. | 一个正数的算术平方根一定大于这个数的相反数 |
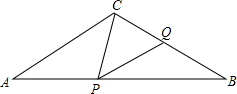 如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.
如图,在△ABC中,AC=BC=10,AB=16,点P在边AB上(不与点A,B重合),作∠CPQ=∠A,PQ交BC于Q,设AP=x,BQ=y.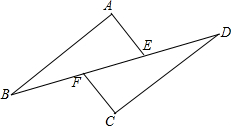 如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明.
如图,AB∥CD,AE∥CF,BF=DE,试找出图中其他的相等关系,并给出证明. 如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.
如图,正方形ABCD,点E是对角线AC上一点,连接BE,过E作EF⊥BE,EF交CD于F,若AE=2$\sqrt{2}$,CF=5,则正方形ABCD的面积为81.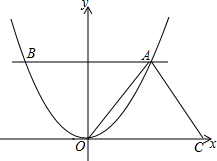 如图,A点是抛物线y=ax2上第一象限内的点,A点坐标为(3,6),AB⊥y轴与抛物线y=ax2的另一交点为B点.
如图,A点是抛物线y=ax2上第一象限内的点,A点坐标为(3,6),AB⊥y轴与抛物线y=ax2的另一交点为B点.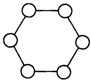 如图,在六边形的顶点处分别标上数1,2,3,4,5,6,能否使任意三个相邻顶点处的三个数之和.
如图,在六边形的顶点处分别标上数1,2,3,4,5,6,能否使任意三个相邻顶点处的三个数之和.