Question

11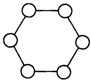．如图，在六边形的顶点处分别标上数1，2，3，4，5，6，能否使任意三个相邻顶点处的三个数之和．
（1）大于9？
（2）大于10？如能，请在图中标出来；若不能，请说明理由．

Answer 1

分析 （1）能，根据题意画出图形，如图所示；
（2）不能，如图，设按要求所填的六个数顺次为a、b、c、d、e、f，根据题意判断即可．

解答 解：（1）能，如图；
（2）不能，
如图，设按要求所填的六个数顺次为a、b、c、d、e、f，
它们任意相邻三数和大于1O，即大于或等于11，
∴a+b+f≥11，b+c+d≥11，c+d+e≥11，d+e+f≥11，e+f+a≥11，f+a+b≥11，
则每个不等式左边相加一定大于或等于66，即3（a+b+c+d+e+f）≥66，
整理得：（a+b+c+d+e+f）≥22，
∵1+2+3+4+5+6=21，
∴与（a+b+c+d+e+f）≥22矛盾，
则不能使每三个相邻的数之和都大于1O．

点评 此题考查了有理数的加法，熟练掌握运算法则是解本题的关键．