题目内容
19.(1)计算:$\sqrt{25}$-|$\root{3}{8}$-1|+(π-2011)0;(2)因式分解:x3-4x2+4x
(3)先化简再求值:($\frac{x}{x-1}$+$\frac{1}{x-1}$)$\frac{1}{x+1}$,其中x=2.
分析 (1)首先计算乘方、开方,然后从左向右依次计算,求出$\sqrt{25}$-|$\root{3}{8}$-1|+(π-2011)0的值是多少即可.
(2)应用提公因式法,把x3-4x2+4x进行因式分解即可.
(3)首先化简($\frac{x}{x-1}$+$\frac{1}{x-1}$)$\frac{1}{x+1}$,然后把x=2代入化简后的算式,求出算式的值是多少即可.
解答 解:(1)$\sqrt{25}$-|$\root{3}{8}$-1|+(π-2011)0
=5-|2-1|+1
=5-1+1
=5
(2)x3-4x2+4x
=x(x2-4x+4)
=x(x-2)2
(3)($\frac{x}{x-1}$+$\frac{1}{x-1}$)$\frac{1}{x+1}$
=$\frac{x+1}{x-1}$•$\frac{1}{x+1}$
=$\frac{1}{x-1}$
当x=2时,
原式=$\frac{1}{2-1}$=1.
点评 此题主要考查了实数的运算,因式分解的方法,以及分式的化简求值问题,要熟练掌握,注意先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
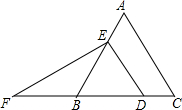 如图,在等边△ABC中,点D、E分别在边BC、AB上,且DE∥AC,过点E作EF⊥DE,交CB的延长线于点F.若BD=5,则EF2=75.
如图,在等边△ABC中,点D、E分别在边BC、AB上,且DE∥AC,过点E作EF⊥DE,交CB的延长线于点F.若BD=5,则EF2=75.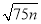 是整数,则正整数n的最小值是( )
是整数,则正整数n的最小值是( ) C. 5或
C. 5或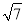 D. 5或6
D. 5或6 如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米,某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标