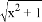题目内容
13.(1)已知a,b是有理数且满足:a是-27的立方根,$\sqrt{{b}^{2}}$=7,求a2+2b的值;(2)已知a-b=2,a-c=$\frac{1}{2}$,求(b-c)2+3(b-c)+$\frac{9}{4}$的值.
分析 (1)根据立方根的意义,算术平方根的性质即可解决问题.
(2)首先求出b-c的值,利用完全平方公式即可解决问题.
解答 解:(1)∵a是-27的立方根,
∴a=-3,
∵$\sqrt{{b}^{2}}$=7,
∴b=±7,
∴a2+2b=23或-5.
(2)∵a-b=2,a-c=$\frac{1}{2}$,
∴b-c=-$\frac{3}{2}$,
∴b-c+$\frac{3}{2}$=0,
∴原式=(b-c+$\frac{3}{2}$)2=0.
点评 本题考查立方根、算术平方根、代数式求值、完全平方公式等知识,解题的关键是掌握基本概念,灵活应用公式解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.把多项式x2+ax+b分解因式,得(x-1)(x+3),则a,b的值分别是( )
| A. | a=2,b=3 | B. | a=2,b=-3 | C. | a=-2,b=3 | D. | a=-2,b=-3 |
18.若a、b互为相反数,则a+b-(-2)的值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | ±2 |
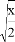 B.
B. 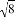 C.
C. 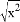 D.
D.