题目内容
12.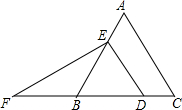 如图,在等边△ABC中,点D、E分别在边BC、AB上,且DE∥AC,过点E作EF⊥DE,交CB的延长线于点F.若BD=5,则EF2=75.
如图,在等边△ABC中,点D、E分别在边BC、AB上,且DE∥AC,过点E作EF⊥DE,交CB的延长线于点F.若BD=5,则EF2=75.
分析 根据平行线的性质可得∠EDB=∠C=60°,进而可证明△EDB是等边三角形,再根据勾股定理即可求解EF的长.
解答 解:∵△ABC是等边三角形,
∴∠C=60°,
∵DE∥AC,
∴∠EDB=∠C=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDB=30°,
∵∠ABC=60°,∠EDB=60°,
∴△EDB是等边三角形.
∴ED=BD=5,
∵∠DEF=90°,∠F=30°,
∴DF=2DE=10,
∴EF2=DF2-DE2=75.
故答案为:75.
点评 本题考查了等边三角形的判定与性质,以及勾股定理的运用和30度的锐角所对的直角边等于斜边的一半的性质,求出DF的长是解题关键.

练习册系列答案
相关题目
1.把多项式x2+ax+b分解因式,得(x-1)(x+3),则a,b的值分别是( )
| A. | a=2,b=3 | B. | a=2,b=-3 | C. | a=-2,b=3 | D. | a=-2,b=-3 |
 ,较长直角边为
,较长直角边为 ,那么
,那么 的值为( )
的值为( )
 B.
B. 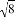 C.
C. 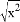 D.
D.