题目内容
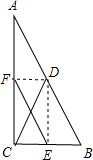 如图,△ABC中,∠ACB=90°,CD是AB上的中线,EF是中位线,下列说法不正确的是( )
如图,△ABC中,∠ACB=90°,CD是AB上的中线,EF是中位线,下列说法不正确的是( )| A、四边形CEDF是矩形 |
| B、CD与EF互相平分 |
| C、CE=CF |
| D、CD=EF |
考点:三角形中位线定理,直角三角形斜边上的中线
专题:
分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得DF∥BC且DF=
BC,然后求出DF∥CE且DF=CE,再根据一组对边平行且相等的四边形是平行四边形判断出四边形CEDF是平行四边形,根据有一个角是直角的平行四边形是矩形判断出四边形CEDF是矩形,然后根据矩形的和平行四边形的性质对各选项分析判断利用排除法求解.
| 1 |
| 2 |
解答:解:∵CD是AB上的中线,EF是中位线,
∴DF是中位线,
∴DF∥BC且DF=
BC,
∵E是BC的中点,
∴CE=
BC,
∴DF∥CE且DF=CE,
∴四边形CEDF是平行四边形,
∵∠ACB=90°,
∴四边形CEDF是矩形,
∴CD与EF互相平分,CD=EF,故A、B、D选项结论正确;
只有AC=BC时,CE=CF,所以,C选项结论不一定正确.
故选C.
∴DF是中位线,
∴DF∥BC且DF=
| 1 |
| 2 |
∵E是BC的中点,
∴CE=
| 1 |
| 2 |
∴DF∥CE且DF=CE,
∴四边形CEDF是平行四边形,
∵∠ACB=90°,
∴四边形CEDF是矩形,
∴CD与EF互相平分,CD=EF,故A、B、D选项结论正确;
只有AC=BC时,CE=CF,所以,C选项结论不一定正确.
故选C.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,矩形的判定与性质,熟记三角形中位线定理以及矩形的判定方法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
永辉超市同时售出两台冷暖空调,每台均卖990元,按成本计算,其中一台盈利10%,另一台亏本10%,则出售这两台空调永辉超市( )
| A、不赔不赚 | B、赚20元 |
| C、亏20元 | D、赚90元 |
下列方程组中方程组是二元一次方程组的是( )
A、
| |||||
B、
| |||||
C、
| |||||
| D、a6•a=a6 |
a2b-4ab+4b因式分解为( )
| A、(a-2)2b |
| B、(2a-2)2b |
| C、(2a-1)2b |
| D、(a+2)2b |
 如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积.
如图,在△ABC中,DE∥BC,AD=3DB,△ABC的面积为72.求:△ADE的面积、四边形DEBC的面积. 如图,这是某市部分简图,为了确定各建筑物的位置:
如图,这是某市部分简图,为了确定各建筑物的位置: