题目内容
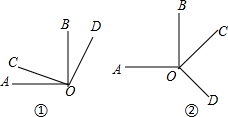
16.∠AOB、∠COD都是直角.(1)如图①,试猜:∠AOC、∠BOD相等吗?
(2)如图①,试猜:∠AOD、∠COB在数量上存在相等、互余还是互补关系?
(3)当∠COD绕点O旋转到如图②的位置,原来的猜想还成立吗?
分析 (1)根据角的和差可以求得∠AOC、∠BOD的大小关系.
(2)根据直角的定义可得∠AOB=∠COD=90°,然后用∠AOD和∠COB表示出∠BOD,列出方程整理即可得解;
(3)根据周角等于360°列式整理即可得解.
解答  解:(1)如图①,相等,理由如下:
解:(1)如图①,相等,理由如下:
∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOC=∠BOD;
(2)∠AOD与∠COB互补.理由如下:
∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∴∠BOD=∠AOD-∠AOB=∠AOD-90°,
∠BOD=∠COD-∠COB=90°-∠COB,
∴∠AOD-90°=90°-∠COB,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补;
(3)成立.理由如下:
∵∠AOB、∠COD都是直角,
∴∠AOB=∠COD=90°,
∵∠AOB+∠BOC+∠COD+∠AOD=360°,
∴∠AOD+∠COB=180°,
∴∠AOD与∠COB互补.
点评 本题考查了余角和补角的定义,比较简单,用两种方法表示出∠BOD是解题的关键.

练习册系列答案
相关题目
 如图,AM∥BN,MC∥ND,求证:PA:PB=PC:PD.
如图,AM∥BN,MC∥ND,求证:PA:PB=PC:PD.