题目内容
5. 如图,AB是⊙O的直径,AE是弦,直线CG与⊙O相切于点C,CG∥AE,CG与BA的延长线交于点G,过点C作CD⊥AB于点D,交AE于点F.
如图,AB是⊙O的直径,AE是弦,直线CG与⊙O相切于点C,CG∥AE,CG与BA的延长线交于点G,过点C作CD⊥AB于点D,交AE于点F.(1)求证:$\widehat{AC}$=$\widehat{CE}$;
(2)若∠EAB=30°,CF=a,写出求四边形GAFC周长的思路.
分析 (1)连接OC,根据切线的性质得到CG⊥OC.根据垂径定理即可得到结论;
(2)连接AC,根据平行线的性质得到∠CGB=30°,推出△AOC是等边三角形,?根据等边三角形的性质得到∠CAF=∠ACF=30°,CF=AF=a,DF=$\frac{1}{2}a$,根据相似三角形的性质得到AG=$\sqrt{3}$a,GC=3a.于是得到结论.
解答 证明:(1)连接OC,如图.
∵直线CG与⊙O相切于点C,
∴CG⊥OC.
∵CG∥AE,
∴AE⊥OC.
又∵OC为⊙O的半径,
∴$\widehat{AC}=\widehat{CE}$;
(2)解:连接AC,如图.
?由∠EAB=30°,CG∥AE,可得∠CGB=30°,
又由直线CG与⊙O相切于点C,∠AOC=60°,
可推出△AOC是等边三角形,
?由△AOC是等边三角形,∠EAB=30°,CF=a,
可得∠CAF=∠ACF=30°,CF=AF=a,DF=$\frac{1}{2}a$,
AD=$\frac{{\sqrt{3}}}{2}a$,
?利用CG∥AE,可得到△ADF∽△GDC,从而推出AG=$\sqrt{3}$a,GC=3a.
故计算出四边形GAFC的周长为5a+$\sqrt{3}$a.
点评 本题考查了切线的性质,等边三角形的判定和性质,相似三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20. 2017年1月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A,B,C,D四个等级,绘制了如图不完整的统计图表.
2017年1月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A,B,C,D四个等级,绘制了如图不完整的统计图表.
根据以上信息解答下列问题:
(1)求m的值;
(2)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
 2017年1月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A,B,C,D四个等级,绘制了如图不完整的统计图表.
2017年1月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A,B,C,D四个等级,绘制了如图不完整的统计图表.| 评估成绩n(分) | 评定等级 | 频数 |
| 90≤n≤100 | A | 2 |
| 80≤n<90 | B | |
| 70≤n<80 | C | 15 |
| n<70 | D | 6 |
(1)求m的值;
(2)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
14.如表为某用户银行存折中2015年11月到2016年5月间代扣水费的相关数据,其中扣缴水费最多的一次的金额为( )
| 日期 | 摘要 | 币种 | 存/取款金额 | 余额 | 操作员 | 备注 |
| 151101 | 北京水费 | RMB钞 | -125.45 | 874.55 | 010005B25 | 折 |
| 160101 | 北京水费 | RMB钞 | -136.02 | 738.53 | 010005Y03 | 折 |
| 160301 | 北京水费 | RMB钞 | -132.36 | 606.17 | 010005D05 | 折 |
| 160501 | 北京水费 | RMB钞 | -128.59 | 477.58 | 01000K19 | 折 |
| A. | 738.53元 | B. | 125.45元 | C. | 136.02元 | D. | 477.58元 |
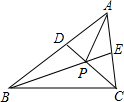 如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AP=PC;④BD+CE=BC;⑤S△PBD+S△PCE=S△PBC,其中正确的个数是( )
如图,任意画一个∠A=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AP=PC;④BD+CE=BC;⑤S△PBD+S△PCE=S△PBC,其中正确的个数是( )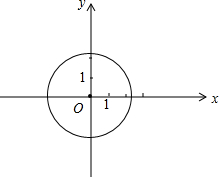 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.