Question

15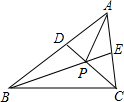．如图，任意画一个∠A=60°的△ABC，再分别作△ABC的两条角平分线BE和CD，BE和CD相交于点P，连接AP，有以下结论：①∠BPC=120°；②AP平分∠BAC；③AP=PC；④BD+CE=BC；⑤S_△PBD+S_△PCE=S_△PBC，其中正确的个数是（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 由三角形内角和定理和角平分线得出∠PBC+∠PCB的度数，再由三角形内角和定理可求出∠BPC的度数，①正确；由∠BPC=120°可知∠DPE=120°，过点P作PF⊥AB，PG⊥AC，PH⊥BC，由角平分线的性质可知AP是∠BAC的平分线，②正确；PF=PG=PH，故∠AFP=∠AGP=90°，由四边形内角和定理可得出∠FPG=120°，故∠DPF=∠EPG，由全等三角形的判定定理可得出△PFD≌△PGE，故可得出PD=PE；由三角形全等的判定定理可得出△BHP≌△BFP，△CHP≌△CGP，故可得出BH=BD+DF，CH=CE-GE，再由DF=EG可得出BC=BD+CE，④正确；可得出S_△PBD+S_△PCE=S_△PBC⑤正确；即可得出结论．

解答 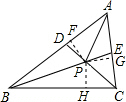解：∵BE、CD分别是∠ABC与∠ACB的角平分线，∠BAC=60°，
∴∠PBC+∠PCB=$\frac{1}{2}$（180°-∠BAC）=$\frac{1}{2}$（180°-60°）=60°，
∴∠BPC=180°-（∠PBC+∠PCB）=180°-60°=120°，①正确；
∵∠BPC=120°，
∴∠DPE=120°，
过点P作PF⊥AB，PG⊥AC，PH⊥BC，
∵BE、CD分别是∠ABC与∠ACB的角平分线，
∴AP是∠BAC的平分线，②正确；PF=PG=PH，
∵∠BAC=60°∠AFP=∠AGP=90°，
∴∠FPG=120°，
∴∠DPF=∠EPG，在△PFD与△PGE中，$\left\{\begin{array}{l}{∠DFP=∠EGP=90°}&{\;}\\{PF=PG}&{\;}\\{∠DPF=∠EPG}&{\;}\end{array}\right.$，
∴△PFD≌△PGE（ASA），
∴PD=PE，
在Rt△BHP与Rt△BFP中，$\left\{\begin{array}{l}{BP=BP}\\{PF=PH}\end{array}\right.$，
∴Rt△BHP≌Rt△BFP（HL），
同理，Rt△CHP≌Rt△CGP，
∴BH=BD+DF，CH=CE-GE，
两式相加得，BH+CH=BD+DF+CE-GE，
∵DF=EG，
∴BC=BD+CE，④正确；
∴S_△PBD+S_△PCE=S_△PBC，⑤正确；
正确的个数有4个，故选：C．

点评 本题考查的是角平分线的性质、全等三角形的判定与性质，根据题意作出辅助线，构造出全等三角形是解答此题的关键．