题目内容
9.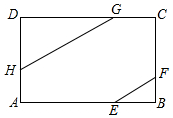 如图所示,F,E,G,H分别在矩形ABCD的四边上,连接EF,GH,且EF∥GH,AH=BF.若AD=3,EF+GH=$\sqrt{34}$,则tan∠DGH=$\frac{3}{5}$.
如图所示,F,E,G,H分别在矩形ABCD的四边上,连接EF,GH,且EF∥GH,AH=BF.若AD=3,EF+GH=$\sqrt{34}$,则tan∠DGH=$\frac{3}{5}$.
分析 先延长GH交BA的延长线于P,连HF,过P作PQ⊥CD,交CD的延长线于Q,根据四边形PEFH为平行四边形,即可得出PG=PH+HG=EF+GH=$\sqrt{34}$,在Rt△PQG中,由勾股定理得QG的长,最后根据解直角三角形即可得到tan∠DGH的值.
解答 解:如图,延长GH交BA的延长线于P,连HF,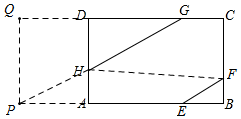
∵AH=BF,AH∥BF,
∴四边形PEFH为平行四边形,
∴EF=PH,
∴PG=PH+HG=EF+GH=$\sqrt{34}$,
如图,过P作PQ⊥CD,交CD的延长线于Q,
∴PQ=AD=3,
在Rt△PQG中,由勾股定理得QG=$\sqrt{P{G}^{2}-P{Q}^{2}}$=5,
∴tan∠DGH═$\frac{PQ}{QG}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题主要考查了矩形的性质以及解直角三角形的运用,解决问题的关键是作辅助线构造平行四边形以及直角三角形,依据平行四边形的性质和勾股定理进行计算.

练习册系列答案
相关题目
4. 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
 如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )
如图,一条公路第一次转弯转的角∠β=140°,若使两次转变后回到原来的方向,∠C应是( )| A. | 140° | B. | 40° | C. | 100° | D. | 180° |
5.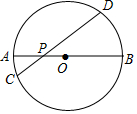 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
 如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )| A. | $\sqrt{15}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{15}$ | D. | 8 |
2.下列说法中,正确的是( )
| A. | 若a≠b,则a2≠b2 | B. | 若a>|b|,则a>b | C. | 若|a|=|b|,则a=b | D. | 若|a|>|b|,则a>b |
18.若代数式(A-$\frac{3}{a-1}$)•$\frac{2a-2}{a+2}$的化简结果为2a-4.则整式A为( )
| A. | a+1 | B. | a-1 | C. | -a-1 | D. | -a+1 |
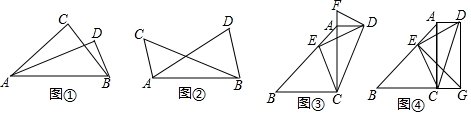
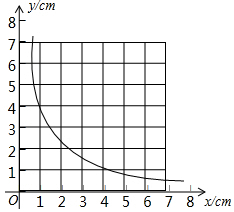 一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题:
一个三角形的面积始终保持不变,它的一边的长为xcm,这边上的高为ycm,y与x的关系如图,根据图中给出的信息,解答下列问题: