��Ŀ����
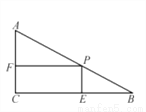
��ͼ����Rt��ABC�У���C=90��,��B=30��,AB=12cm����P��AB���ϵ�һ�����㣬����P��PE��BC�ڵ�E,PF��AC�ڵ�F,��PB=6cmʱ���ı���PECF�����������ֵΪ______
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ����Rt��ABC�У���C=90��,��B=30��,AB=12cm����P��AB���ϵ�һ�����㣬����P��PE��BC�ڵ�E,PF��AC�ڵ�F,��PB=6cmʱ���ı���PECF�����������ֵΪ______
